Question

【题目】如图，在平面直角坐标xOy中，正比例函数y=kx的图象与反比例函数y= 的图象都经过点A（2，﹣2）．

（1）分别求这两个函数的表达式；
（2）将直线OA向上平移3个单位长度后与y轴交于点B，与反比例函数图象在第四象限内的交点为C，连接AB，AC，求点C的坐标及△ABC的面积．

Answer 1

【答案】
（1）

解：根据题意，将点A（2，﹣2）代入y=kx，得：﹣2=2k，

解得：k=﹣1，

∴正比例函数的解析式为：y=﹣x，

将点A（2，﹣2）代入y= ，得：﹣2= ，

解得：m=﹣4；

∴反比例函数的解析式为：y=﹣ ；

（2）

解：直线OA：y=﹣x向上平移3个单位后解析式为：y=﹣x+3，

则点B的坐标为（0，3），

联立两函数解析式 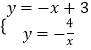，解得： 或 ，

∴第四象限内的交点C的坐标为（4，﹣1），

∴S△ABC= ×（1+5）×4﹣ ×5×2﹣ ×2×1=6

【解析】（1）将点A坐标（2，﹣2）分别代入y=kx、y= 求得k、m的值即可；（2）由题意得平移后直线解析式，即可知点B坐标，联立方程组求解可得第四象限内的交点C得坐标，割补法求解可得三角形的面积．此题考查了反比例函数与一次函数的交点问题，涉及的知识有：坐标与图形性质，直线与坐标轴的交点，待定系数法求函数解析式，熟练掌握待定系数法是解本题的关键．