练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，半径为3的⊙O与Rt△AOB的斜边AB切于点D，交OB于点C，连接CD交直线OA于点E，若∠B=30°，则线段AE的长为 ．

    【答案】
    【解析】解：连接OD，如右图所示，

    由已知可得，∠BOA=90°，OD=OC=3，∠B=30°，∠ODB=90°，
    ∴BO=2OD=6，∠BOD=60°，
    ∴∠ODC=∠OCD=60°，AO=BOtan30°= ，
    ∵∠COE=90°，OC=3，
    ∴OE=OCtan60°= ，∴AE=OE﹣OA= ，所以答案是： ．
    【考点精析】本题主要考查了切线的性质定理的相关知识点，需要掌握切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，把一个菱形绕着它的对角线的交点旋转90°，旋转前后的两个菱形构成一个“星形”（阴影部分），若菱形的一个内角为60°，边长为2，则该“星形”的面积是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，抛物线y=a（x+1）2﹣3与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C（0，﹣ ），顶点为D，对称轴与x轴交于点H，过点H的直线l交抛物线于P，Q两点，点Q在y轴的右侧．

    （1）求a的值及点A，B的坐标；
    （2）当直线l将四边形ABCD分为面积比为3：7的两部分时，求直线l的函数表达式；
    （3）当点P位于第二象限时，设PQ的中点为M，点N在抛物线上，则以DP为对角线的四边形DMPN能否为菱形？若能，求出点N的坐标；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，随着我市铁路建设进程的加快，现规划从A地到B地有一条笔直的铁路通过，但在附近的C处有一大型油库，现测得油库C在A地的北偏东60°方向上，在B地的西北方向上，AB的距离为250（ +1）米．已知在以油库C为中心，半径为200米的范围内施工均会对油库的安全造成影响．问若在此路段修建铁路，油库C是否会受到影响？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，轮船沿正南方向以30海里/时的速度匀速航行，在M处观测到灯塔P在西偏南68°方向上，航行2小时后到达N处，观测灯塔P在西偏南46°方向上，若该船继续向南航行至离灯塔最近位置，则此时轮船离灯塔的距离约为（由科学计算器得到sin68°=0.9272，sin46°=0.7193，sin22°=0.3746，sin44°=0.6947）（　　）

    A.22.48
    B.41.68
    C.43.16
    D.55.63

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，正方形OABC的顶点O与坐标原点重合，点C的坐标为（0，3），点A在x轴的负半轴上，点D、M分别在边AB、OA上，且AD=2DB，AM=2MO，一次函数y=kx+b的图象过点D和M，反比例函数y= 的图象经过点D，与BC的交点为N．

    （1）求反比例函数和一次函数的表达式；
    （2）若点P在直线DM上，且使△OPM的面积与四边形OMNC的面积相等，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，请你添加一个适当的条件： ， 使△AEH≌△CEB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，△ABC和△DEF中，AB=AC，DE=DF，∠A=∠D．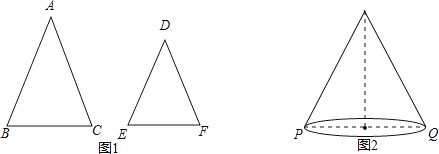

    （1）求证： ；
    （2）由（1）中的结论可知，等腰三角形ABC中，当顶角∠A的大小确定时，它的对边（即底边BC）与邻边（即腰AB或AC）的比值也就确定，我们把这个比值记作T（A），即T（A）= 的对边（底边）/的领边（腰）= ，如T（60°）=1．
    ①理解巩固：T（90°）= ， T（120°）= ， 若α是等腰三角形的顶角，则T（α）的取值范围是；
    ②学以致用：如图2，圆锥的母线长为9，底面直径PQ=8，一只蚂蚁从点P沿着圆锥的侧面爬行到点Q，求蚂蚁爬行的最短路径长（精确到0.1）．
    （参考数据：T（160°）≈1.97，T（80°）≈1.29，T（40°）≈0.68）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，正方形ABCD的顶点分别为A（1，1）、B（1，﹣1）、C（﹣1，﹣1）、D（﹣1，1），y轴上有一点P（0，2）．作点P关于点A的对称点P1 ， 作P1关于点B的对称点P2 ， 作点P2关于点C的对称点P3 ， 作P3关于点D的对称点P4 ， 作点P4关于点A的对称点P5 ， 作P5关于点B的对称点P6┅，按如此操作下去，则点P2011的坐标为（ ）
    A.（0，2）
    B.（2，0）
    C.（0，﹣2）
    D.（﹣2，0）

    查看答案和解析>>

    同步练习册答案