
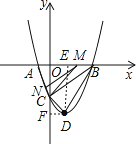
ЁОЬтФПЁПвбжЊХзЮяЯпy=x2+bx+cОЙ§AЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉСНЕуЃЌгыyжсЯрНЛгкЕуCЃЌИУХзЮяЯпЕФЖЅЕуЮЊЕуD
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФНтЮіЪНМАЕуDЕФзјБъЁЃ
ЃЈ2ЃЉСЌНгACЃЌCDЃЌBDЃЌBCЃЌЩшЁїAOCЃЌЁїBOCЃЌЁїBCDЕФУцЛ§ЗжБ№ЮЊS1 ЃЌ S2КЭS3 ЃЌ гУЕШЪНБэЪОS1 ЃЌ S2 ЃЌ S3жЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩ
ЃЈ3ЃЉМйЩшДцдкЃЌЩшЕуMЕФзјБъЮЊЃЈmЃЌ0ЃЉЃЌБэЪОГіMAЕФГЄЃЌИљОнMNЁЮBCЃЌЕУЕНБШР§ЪНЧѓГіANЃЌИљОнЁїAMNЁзЁїACMЃЌЕУЕНБШР§ЪНЧѓГіmЃЌЕУЕНЕуMЕФзјБъЃЌЧѓГіBCЕФНтЮіЪНЃЌИљОнMNЁЮBCЃЌЩшжБЯпMNЕФНтЮіЪНЃЌЧѓНтМДПЩ
ЁОД№АИЁП
ЃЈ1ЃЉ
НтЃКЁпХзЮяЯпy=x2+bx+cОЙ§AЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉСНЕуЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЎ
ЃЎ
ЁрХзЮяЯпЕФНтЮіЪНЮЊЃКy=x2Љ2xЉ3ЃЌ
y=x2Љ2xЉ3=ЃЈxЉ1ЃЉ2Љ4ЃЌ
ЁрЕуDЕФзјБъЮЊЃКЃЈ1ЃЌЉ4ЃЉ
ЃЈ2ЃЉ
НтЃКS1+S3=S2ЃЌ
Й§ЕуDзїDEЁЭxжсгкЕуEЃЌDFЁЭyжсгкFЃЌ
гЩЬтвтЕУЃЌCD=![]() ЃЌBD=
ЃЌBD=![]() ЃЌBC=
ЃЌBC=![]() ЃЌ
ЃЌ
CD2+BC2=BD2ЃЌ
ЁрЁїBCDЪЧжБНЧШ§НЧаЮЃЌ
S1=![]() ЁСOAЁСOC=
ЁСOAЁСOC=![]() ЃЌ
ЃЌ
S2=![]() ЁСOBЁСOC=
ЁСOBЁСOC=![]()
S3=![]() ЁСCDЁСBC=3ЃЌ
ЁСCDЁСBC=3ЃЌ
ЁрS1+S3=S2
ЃЈ3ЃЉ
НтЃКДцдкЕуMЪЙЁЯAMN=ЁЯACMЃЌ
ЩшЕуMЕФзјБъЮЊЃЈmЃЌ0ЃЉЃЌ
ЁпЉ1ЃМmЃМ3ЃЌ
ЁрMA=m+1ЃЌAC=![]() ЃЌ
ЃЌ
ЁпMNЁЮBCЃЌ
Ёр![]() =
=![]() ЃЌМД
ЃЌМД![]() =
=![]() ЃЌ
ЃЌ
НтЕУЃЌAN=![]() ЃЈm+1ЃЉЃЌ
ЃЈm+1ЃЉЃЌ
ЁпЁЯAMN=ЁЯACMЃЌЁЯMAN=ЁЯCAMЃЌ
ЁрЁїAMNЁзЁїACMЃЌ
Ёр![]() =
=![]() ЃЌМДЃЈm+1ЃЉ2=
ЃЌМДЃЈm+1ЃЉ2=![]()
![]() ЃЈm+1ЃЉЃЌ
ЃЈm+1ЃЉЃЌ
НтЕУЃЌm1=![]() ЃЌm2=Љ1ЃЈЩсШЅЃЉЃЌ
ЃЌm2=Љ1ЃЈЩсШЅЃЉЃЌ
ЁрЕуMЕФзјБъЮЊЃЈ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
ЩшBCЕФНтЮіЪНЮЊy=kx+bЃЌАбBЃЈ3ЃЌ0ЃЉЃЌCЃЈ0ЃЌЉ3ЃЉДњШыЕУЃЌ
![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
дђBCЕФНтЮіЪНЮЊy=xЉ3ЃЌгжMNЁЮBCЃЌ
ЁрЩшжБЯпMNЕФНтЮіЪНЮЊy=x+bЃЌАбЕуMЕФзјБъЮЊЃЈ![]() ЃЌ0ЃЉДњШыЕУЃЌ
ЃЌ0ЃЉДњШыЕУЃЌ
b=Љ![]() ЃЌ
ЃЌ
ЁржБЯпMNЕФНтЮіЪНЮЊy=xЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁПЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіХзЮяЯпЕФНтЮіЪНЃЌгУХфЗНЗЈАбвЛАуЪНЛЏЮЊЖЅЕуЪНЧѓГіЕуDЕФзјБъЃЛ
ЃЈ2ЃЉИљОнЕуЕФзјБъЧѓГіЁїAOCЃЌЁїBOCЕФУцЛ§ЃЌРћгУЙДЙЩЖЈРэЕФФцЖЈРэХаЖЯЁїBCDЮЊжБНЧШ§НЧаЮЃЌЧѓГіЦфУцЛ§ЃЌМЦЫуМДПЩЕУЕНД№АИЃЛ
ЃЈ3ЃЉМйЩшДцдкЃЌЩшЕуMЕФзјБъЮЊЃЈmЃЌ0ЃЉЃЌБэЪОГіMAЕФГЄЃЌИљОнMNЁЮBCЃЌЕУЕНБШР§ЪНЧѓГіANЃЌИљОнЁїAMNЁзЁїACMЃЌЕУЕНБШР§ЪНЧѓГіmЃЌЕУЕНЕуMЕФзјБъЃЌЧѓГіBCЕФНтЮіЪНЃЌИљОнMNЁЮBCЃЌЩшжБЯпMNЕФНтЮіЪНЃЌЧѓНтМДПЩЃЎ
ЁОПМЕуОЋЮіЁПНтД№ДЫЬтЕФЙиМќдкгкРэНтЯрЫЦШ§НЧаЮЕФаджЪЕФЯрЙижЊЪЖЃЌеЦЮеЖдгІНЧЯрЕШЃЌЖдгІБпГЩБШР§ЕФСНИіШ§НЧаЮНазіЯрЫЦШ§НЧаЮЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌЕуEЁЂFЗжБ№дкБпADЁЂBCЩЯЃЌЧвEFЁЮCDЃЌGЮЊБпADбгГЄЯпЩЯвЛЕуЃЌСЌНгBGЃЌдђЭМжагыЁїABGЯрЫЦЕФШ§НЧаЮгаЃЈ ЃЉИіЃЎ 
A.1
B.2
C.3
D.4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊКЏЪ§![]() ЕФЭМЯѓгыxжсЁЂyжсЗжБ№НЛгкЕуAЃЌBЃЌгыКЏЪ§yЃНxЕФЭМЯѓНЛгкЕуMЃЌЕуMЕФКсзјБъЮЊ2ЃЎдкxжсЩЯгавЛЕуP (aЃЌ0)ЃЈЦфжаa>2ЃЉЃЌЙ§ЕуPзїxжсЕФДЙЯпЃЌЗжБ№НЛКЏЪ§
ЕФЭМЯѓгыxжсЁЂyжсЗжБ№НЛгкЕуAЃЌBЃЌгыКЏЪ§yЃНxЕФЭМЯѓНЛгкЕуMЃЌЕуMЕФКсзјБъЮЊ2ЃЎдкxжсЩЯгавЛЕуP (aЃЌ0)ЃЈЦфжаa>2ЃЉЃЌЙ§ЕуPзїxжсЕФДЙЯпЃЌЗжБ№НЛКЏЪ§![]() КЭyЃНxЕФЭМЯѓгкЕуCЃЌDЃЎ
КЭyЃНxЕФЭМЯѓгкЕуCЃЌDЃЎ
ЃЈ1ЃЉЧѓЕуAЕФзјБъЃЛ
ЃЈ2ЃЉШєOBЃНCDЃЌЧѓaЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЪЧБпГЄЮЊ2ЃЌвЛИіШёНЧЕШгк60ЁуЕФСтаЮжНЦЌЃЌаЁЗМЭЌбЇНЋвЛИіШ§НЧаЮжНЦЌЕФвЛИіЖЅЕугыИУСтаЮЖЅЕуDжиКЯЃЌАДЫГЪБеыЗНЯђа§зЊШ§НЧаЮжНЦЌЃЌЪЙЫќЕФСНБпЗжБ№НЛCBЁЂBAЃЈЛђЫќУЧЕФбгГЄЯпЃЉгкЕуEЁЂFЃЌЁЯEDF=60ЁуЃЌЕБCE=AFЪБЃЌШчЭМ1аЁЗМЭЌбЇЕУГіЕФНсТлЪЧDE=DFЃЎ
ЃЈ1ЃЉМЬаја§зЊШ§НЧаЮжНЦЌЃЌЕБCEЁйAFЪБЃЌШчЭМ2аЁЗМЕФНсТлЪЧЗёГЩСЂЃПШєГЩСЂЃЌМгвджЄУїЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩ
ЃЈ2ЃЉдйДЮа§зЊШ§НЧаЮжНЦЌЃЌЕБЕуEЁЂFЗжБ№дкCBЁЂBAЕФбгГЄЯпЩЯЪБЃЌШчЭМ3ЧыжБНгаДГіDEгыDFЕФЪ§СПЙиЯЕЃЛ
ЃЈ3ЃЉСЌEFЃЌШєЁїDEFЕФУцЛ§ЮЊyЃЌCE=xЃЌЧѓyгыxЕФЙиЯЕЪНЃЌВЂжИГіЕБxЮЊКЮжЕЪБЃЌyгазюаЁжЕЃЌзюаЁжЕЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇаЃЮЊСЫНтЦпФъМЖФаЩњЬхжЪНЁПЕЧщПіЃЌЫцЛњГщШЁШєИЩУћФаЩњНјааВтЪдЃЌВтЪдНсЙћЗжЮЊгХауЁЂСМКУЁЂКЯИёЁЂВЛКЯИёЫФИіЕШМЖЃЌЭГМЦећРэЪ§ОнВЂЛцжЦЭМ1ЁЂЭМ2СНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыИљОнЭМжааХЯЂЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБОДЮНгЪеЫцЛњГщбљЕїВщЕФФаЩњШЫЪ§ЮЊ ШЫЃЌЩШаЮЭГМЦЭМжаЁАСМКУЁБЫљЖдгІЕФдВаФНЧЕФЖШЪ§ЮЊ ЁЃ
ЃЈ2ЃЉВЙШЋЬѕаЮЭГМЦЭМжаЁАгХауЁБЕФПеШБВПЗжЁЃ
ЃЈ3ЃЉШєИУаЃЦпФъМЖЙВгаФаЩњ480ШЫЃЌЧыЙРМЦШЋФъМЖФаЩњЬхжЪНЁПЕзДПіДяЕНЁАСМКУЁБЕФШЫЪ§
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЮЊЁбOЕФжБОЖЃЌAB=ACЃЌBCНЛЁбOгкЕуDЃЌACНЛЁбOгкЕуEЃЌЁЯBAC=45ЁуЃЌИјГівдЯТЮхИіНсТлЃКЂйЁЯEBC=22.5ЁуЃЛЂкBD=DCЃЛЂлAE=2ECЃЛЂмСгЛЁ![]() ЪЧСгЛЁ
ЪЧСгЛЁ![]() ЕФ2БЖЃЛЂнAE=BCЃЌЦфжае§ШЗЕФађКХЪЧ
ЕФ2БЖЃЛЂнAE=BCЃЌЦфжае§ШЗЕФађКХЪЧ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌЕуCЪЧ![]() ЕФжаЕуЃЌЁбOЕФЧаЯпBDНЛACЕФбгГЄЯпгкЕуDЃЌEЪЧOBЕФжаЕуЃЌCEЕФбгГЄЯпНЛЧаЯпBDгкЕуFЃЌAFНЛЁбOгкЕуHЃЌСЌНгBHЃЎ
ЕФжаЕуЃЌЁбOЕФЧаЯпBDНЛACЕФбгГЄЯпгкЕуDЃЌEЪЧOBЕФжаЕуЃЌCEЕФбгГЄЯпНЛЧаЯпBDгкЕуFЃЌAFНЛЁбOгкЕуHЃЌСЌНгBHЃЎ
ЃЈ1ЃЉЧѓжЄЃКAC=CD;
ЃЈ2ЃЉШєOC=![]() ЃЌЧѓBHЕФГЄ.
ЃЌЧѓBHЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПДгЉ3ЃЌЉ1ЃЌ ![]() ЃЌ1ЃЌ3етЮхИіЪ§жаЃЌЫцЛњГщШЁвЛИіЪ§ЃЌМЧЮЊaЃЌШєЪ§aЪЙЙигкxЕФВЛЕШЪНзщ
ЃЌ1ЃЌ3етЮхИіЪ§жаЃЌЫцЛњГщШЁвЛИіЪ§ЃЌМЧЮЊaЃЌШєЪ§aЪЙЙигкxЕФВЛЕШЪНзщ  ЮоНтЃЌЧвЪЙЙигкxЕФЗжЪНЗНГЬ
ЮоНтЃЌЧвЪЙЙигкxЕФЗжЪНЗНГЬ ![]() Љ
Љ ![]() =Љ1гаећЪ§НтЃЌФЧУДет5ИіЪ§жаЫљгаТњзуЬѕМўЕФaЕФжЕжЎКЭЪЧЃЈЁЁЁЁЃЉ
=Љ1гаећЪ§НтЃЌФЧУДет5ИіЪ§жаЫљгаТњзуЬѕМўЕФaЕФжЕжЎКЭЪЧЃЈЁЁЁЁЃЉ
A.Љ3
B.Љ2
C.Љ ![]()
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌЁЯBACЕФЦНЗжЯпНЛBCгкЕуOЃЌOC=1ЃЌвдЕуOЮЊдВаФOCЮЊАыОЖзїАыдВЃЎ
ЃЈ1ЃЉЧѓжЄЃКABЮЊЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШчЙћtanЁЯCAO= ![]() ЃЌЧѓcosBЕФжЕЃЎ
ЃЌЧѓcosBЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com