
【题目】如图,四边形ABCD是边长为2,一个锐角等于60°的菱形纸片,小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合,按顺时针方向旋转三角形纸片,使它的两边分别交CB、BA(或它们的延长线)于点E、F,∠EDF=60°,当CE=AF时,如图1小芳同学得出的结论是DE=DF.
(1)继续旋转三角形纸片,当CE≠AF时,如图2小芳的结论是否成立?若成立,加以证明;若不成立,请说明理由
(2)再次旋转三角形纸片,当点E、F分别在CB、BA的延长线上时,如图3请直接写出DE与DF的数量关系;
(3)连EF,若△DEF的面积为y,CE=x,求y与x的关系式,并指出当x为何值时,y有最小值,最小值是多少?
【答案】
(1)
解:DF=DE.理由如下:

如答图1,连接BD.
∵四边形ABCD是菱形,
∴AD=AB.
又∵∠DAB=60°,
∴△ABD是等边三角形,
∴AD=BD,∠ADB=60°,
∴∠DBE=∠DAF=60°
∵∠EDF=60°,
∴∠ADF=∠BDE.∵在△ADF与△BDE中,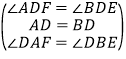 ,
,
∴△ADF≌△BDE(ASA),
∴DF=DE;
(2)
解:DF=DE.理由如下:
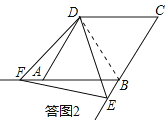
如答图2,连接BD.∵四边形ABCD是菱形,
∴AD=AB.
又∵∠DAB=60°,
∴△ABD是等边三角形,
∴AD=BD,∠ADB=60°,
∴∠DBE=∠DAF=60°
∵∠EDF=60°,
∴∠ADF=∠BDE.
∵在△ADF与△BDE中,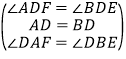 ,
,
∴△ADF≌△BDE(ASA),
∴DF=DE;
(3)
解:

由(2)知,DE=DF,又∵∠EDF=60°,
∴△DEF是等边三角形,
∵四边形ABCD是边长为2的菱形,
∴DH=![]() ,
,
∵BF=CE=x,
∴AF=x﹣2,
∴FH=AF+AH=x﹣2+1=x﹣1,
∴DF=![]() =
=![]() ,DG=
,DG=![]() ×
×![]() ,
,
∴y=S△DEF=![]() ×EF×DG=
×EF×DG=![]() ×
×![]() ×
×![]() ×
×![]() =
=![]() (x﹣1)2+
(x﹣1)2+![]() .
.
∴当x=1时,y最小值=![]() .
.
【解析】(1)如答图1,连接BD.根据题干条件首先证明∠ADF=∠BDE,然后证明△ADF≌△BDE(ASA),得DF=DE;
(2)如答图2,连接BD.根据题干条件首先证明∠ADF=∠BDE,然后证明△ADF≌△BDE(ASA),得DF=DE;
(3)根据(2)中的△ADF≌△BDE得到:△DEF是等边三角形,AF=BE.所以要表示△DEF的面积需要用含x的代数式把底EF和高DG表示出来.据此列出y关于x的二次函数,通过求二次函数的最值来求y的最小值.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图(1)所示,已知四边形SBCD是由直角△SAB和直角梯形ABCD拼接而成的,其中∠SAB=∠SDC=90°,且点A为线段SD的中点,AD=2DC=1,AB=SD,现将△SAB沿AB进行翻折,使得二面角S﹣AB﹣C的大小为90°,得到的图形如图(2)所示,连接SC,点E、F分别在线段SB、SC上. 
(1)证明:BD⊥AF;
(2)若三棱锥B﹣AEC的体积是四棱锥S﹣ABCD体积的 ![]() ,求点E到平面ABCD的距离.
,求点E到平面ABCD的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华和小丽两人玩数字游戏,先由小丽心中任意想一个数字记为x,再由小华猜小丽刚才想的数字,把小华猜的数字记为y,且他们想和猜的数字只能在1,2,3,4这四个数中.
(1)请用树状图或列表法表示了他们想和猜的所有情况;
(2)如果他们想和猜的数相同,则称他们“心灵相通”.求他们“心灵相通”的概率;
(3)如果他们想和猜的数字满足|x﹣y|≤1,则称他们“心有灵犀”.求他们“心有灵犀”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明文具厂工人的工作时间:每月26天,每天8小时.待遇:按件计酬,多劳多得,每月另加福利工资920元,按月结算.该厂生产A,B两种型号零件,工人每生产一件A种型号零件,可得报酬0.85元,每生产一件B种型号零件,可得报酬1.5元,下表记录的是工人小王的工作情况:
生产A种型号零件/件 | 生产B种型号零件/件 | 总时间/分 |
2 | 2 | 70 |
6 | 4 | 170 |
根据上表提供的信息,请回答如下问题:
(1)小王每生产一件A种型号零件、每生产一件B种型号零件,分别需要多少分钟?
(2)设小王某月生产A种型号零件x件,该月工资为y元,求y与x的函数关系式;
(3)如果生产两种型号零件的数目无限制,那么小王该月的工资数目最多为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个18米高的楼顶上有一信号塔DC,李明同学为了测量信号塔的高度,在地面的A处测的信号塔下端D的仰角为30°,然后他正对塔的方向前进了18米到达地面的B处,又测得信号塔顶端C的仰角为60°,CD⊥AB与点E,E、B、A在一条直线上.请你帮李明同学计算出信号塔CD的高度(结果保留整数,![]() ≈1.7,
≈1.7,![]() ≈1.4 ).
≈1.4 ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
①当x>3时,y<0;②3a+b<0;③﹣1≤a≤﹣![]() ;④4ac﹣b2>8a;
;④4ac﹣b2>8a;
其中正确的结论是( )
A.①③④
B.①②③
C.①②④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c经过A(﹣1,0),B(3,0)两点,与y轴相交于点C,该抛物线的顶点为点D
(1)求该抛物线的解析式及点D的坐标。
(2)连接AC,CD,BD,BC,设△AOC,△BOC,△BCD的面积分别为S1 , S2和S3 , 用等式表示S1 , S2 , S3之间的数量关系,并说明理由
(3)假设存在,设点M的坐标为(m,0),表示出MA的长,根据MN∥BC,得到比例式求出AN,根据△AMN∽△ACM,得到比例式求出m,得到点M的坐标,求出BC的解析式,根据MN∥BC,设直线MN的解析式,求解即可
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的分式方程 ![]() ﹣3=
﹣3= ![]() 有负分数解,且关于x的不等式组
有负分数解,且关于x的不等式组  的解集为x<﹣2,那么符合条件的所有整数a的积是( )
的解集为x<﹣2,那么符合条件的所有整数a的积是( )
A.﹣3
B.0
C.3
D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月27日“丽水半程马拉松竞赛”在莲都举行,某运动员从起点万地广场西门出发,途经紫金大桥,沿比赛路线跑回中点万地广场西门.设该运动员离开起点的路程S(千米)与跑步时间t(分钟)之间的函数关系如图所示,其中从起点到紫金大桥的平均速度是0.3千米/分,用时35分钟,根据图象提供的信息,解答下列问题:
(1)求图中a的值;
(2)组委会在距离起点2.1千米处设立一个拍摄点C,该运动员从第一次经过C点到第二次经过C点所用的时间为68分钟.
①求AB所在直线的函数解析式;
②该运动员跑完赛程用时多少分钟?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com