Question

已知A，B两地相距120千米，甲、乙两车分别从A，B两地同时出发，相向而行，其终点分别为B，A两地．两车均先以a千米每小时的速度行驶，再以b千米每小时的速度行驶，且甲车以两种速度行驶的路程相等，乙车以两种速度行驶的时间相等．
（1）若b=a，且甲车行驶的总时间为小时，求a和b的值；
（2）若b-a=30，且乙车行驶的总时间为小时．
①求a和b的值；
②求两车相遇时，离A地多少千米．

Answer 1

解：（1）由题意，得
，
解得：，
答：a的值为80千米/时，b的值为120千米/时．
（1）①由题意，得
，
解得：．
∴a=60，b=90；
②由题意，得
相遇时甲行驶的时间为：+（120-×2）÷（60+90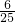）=（+）小时；
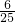∴乙离A地距离，即为甲行驶的距离为：（+）×60=62.4千米 答：两车相遇时，离A地62.4千米．
分析：（1）由甲车以两种速度行驶的路程相等且时间为小时及b=a建立方程组求出其解即可；
（2）①由乙车行驶的时间相等就可以得出两次的时间分别为小时，由两段路程之和等于120及b-a=30建立方程组求出其解即可求出a、b的值，
②当行驶前小时，甲乙两车均以60千米每小时的速度行驶．两车分别行驶48千米，即一共行驶了96千米．当行驶道1小时时，甲车以60千米每小时行驶，乙车以90千米每小时行驶．在这段时间甲车可以行驶12千米，乙车可以行驶18千米．共行驶30.30+96=126＞120，说明两车相遇是在这个时间段．则相遇时，两车以这样的速度已经行驶了：（120-96）÷（60+90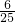）=小时．1小时以后两车均以90千米每小时行驶，直到行驶至目的地．由条件就可以求出结论．
综上所述，两车相遇时，乙离A地距离，即为甲行驶的距离：
点评：本题考查了行程问题的数量关系的运用，列二元一次方程解实际问题的运用，解答时分别运用路程相等和时间相等建立方程组是解答本题的关键．