
【题目】“滴滴”已成为一种出行习惯,其中的“滴滴专车”正成为非常热门的出行选择.经了解温州地区滴滴专车部分计价规则如下表:
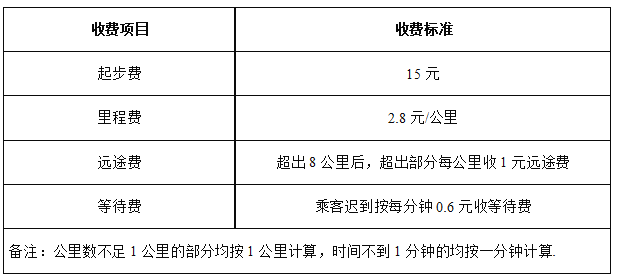
以没有收取等待费为例:某甲坐车10公里的费用为15+2.8×10+1×(10-8)=45元
(1)若行驶里程为6千米,且没有收取等待费,求应支付的总费用;
(2)若某天小周迟到7分钟才上车,且里程数超过了8公里,最终支付的总费用为53元,求支付的远途费;
(3)某次行程结束后,乘客小周发现乘车的里程数超过了5公里,需要支付的费用恰好为46元,起初小周认为系统计算错误,经司机提醒才记起,原来是他有事耽搁没有及时上车,被收取了等待费,则收取的等待费为 元.(直接在横线上写出答案)
【答案】(1)31.8元;(2)3元;(3)4.8 ,11.4
【解析】试题分析:(1)按照题意计算即可;(2)根据题意列出一元一次方程15+2.8x+1×(x-8)+0.6×7=53,结合实际情况求解;(3)根据题意,分两种情况列出二元一次方程15+2.8x+0.6y=46和15+2.8x+1×(x-8)+0.6×7=46,结合实际情况求解;
(1)15+2.8×6=31.8(元);
(2)设里程数是x千米,由题意得,
15+2.8x+1×(x-8)+0.6×7=53,
解之得
x=11
1×(11-8)=3(元)
(3)设里程数是x千米,等待了y分钟.
当5<x≤8时,由题意得
15+2.8x+0.6y=46,
解之得
![]() ,
,
∴等待费为:19×0.6=11.4(元).
当x>8时,由题意得
15+2.8x+1×(x-8)+0.6y=46,
解之得
![]() ,
,
∴等待费为:8×0.6=4.8(元).
故等待费为4.8元或11.4元.


科目:初中数学 来源: 题型:
【题目】已知:如图,点C在AOB的一边OA上,过点C的直线DE//OB,CF平分ACD,CG CF于C .
(1)若O =40,求ECF的度数;
(2)求证:CG平分OCD;
(3)当O为多少度时,CD平分OCF,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名学生军训时连续射靶10次,命中环数分别为 7,8,6,8,5,9,10,7,6,4.则这名学生射击环数的方差是( )
A. 3 B. 2.9 C. 2.8 D. 2.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】保障房建设是民心工程,某市从2012年开始加快保障房建设进程,现统计了该市2012年到2016年这5年新建保障房情况,绘制成如图所示的折线统计图和不完整的条形统计图.
 (1)小丽看了统计图后说:“该市2015年新建保障房的套数比2014年少了.”你认为小丽的说法正确吗?请说明理由;
(1)小丽看了统计图后说:“该市2015年新建保障房的套数比2014年少了.”你认为小丽的说法正确吗?请说明理由;
(2)请补全条形统计图;
(3)求这5年平均每年新建保障房的套数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=![]() (x>0)的图象与BC边交于点E.
(x>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中有三个点A,B,C,要求作一个四边形使这三个点在这个四边形的边(包括顶点)上,且四边形的顶点在方格的顶点上. 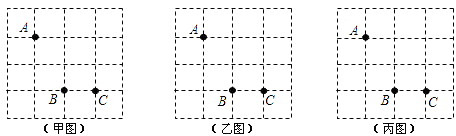
(1)在甲图中作出的四边形是中心对称图形但不是轴对称图形;
(2)在乙图中作出的四边形是轴对称图形但不是中心对称图形;
(3)在丙图中作出的四边形既是轴对称图形又是中心对称图形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com