
 如图所示,△ABC和△CDE是等边三角形,E是AC延长线上一点,M是AD的中点,N是BE的中点.试说明:△CMN是等边三角形.
如图所示,△ABC和△CDE是等边三角形,E是AC延长线上一点,M是AD的中点,N是BE的中点.试说明:△CMN是等边三角形. 分析 根据△ACD≌△BCE,得出AD=BE,AM=BN;又△AMC≌△BNC,可得CM=CN,∠ACM=∠BCN,证明∠NCM=∠ACB=60°即可证明△CMN是等边三角形.
解答 证明:∵△ABC是等边三角形,△CDE是等边三角形,M是线段AD的中点,N是线段BE的中点,
∴∠ACB=∠ECD=60°,
∴∠ACB+∠BCD=∠ECD+∠BCD,即∠ACD=∠BCE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE,
∴AD=BE,AM=BN;
∴AC=BC,∠CAD=∠CBE,
在△AMC和△BNC中
$\left\{\begin{array}{l}{AM=BN}\\{∠MAC=∠NBC}\\{AC=BC}\end{array}\right.$
∴△AMC≌△BNC(SAS),
∴CM=CN,∠ACM=∠BCN;
又∵∠NCM=∠BCN-∠BCM,
∠ACB=∠ACM-∠BCM,
∴∠NCM=∠ACB=60°,
∴△CMN是等边三角形.
点评 本题考查了等边三角形的判定与性质及全等三角形的判定与性质,难度一般,熟练掌握等边三角形的性质是解答的关键.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
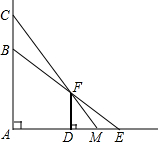 如图,一只猫头鹰蹲在树AC上的B处,通过墙顶F发现一只老鼠在E处,刚想起飞捕捉时,老鼠突然跑到矮墙DF的阴影下,猫头鹰立即从B处向上飞至树上C处时,恰巧可以通过墙顶F看到老鼠躲在M处(A、D、M、E四点在同一条直线上).
如图,一只猫头鹰蹲在树AC上的B处,通过墙顶F发现一只老鼠在E处,刚想起飞捕捉时,老鼠突然跑到矮墙DF的阴影下,猫头鹰立即从B处向上飞至树上C处时,恰巧可以通过墙顶F看到老鼠躲在M处(A、D、M、E四点在同一条直线上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知等边三角形ABC,D为AC上一点,CD=CE,∠ACE=60°,延长BD交AE于F,连接CF.
如图,已知等边三角形ABC,D为AC上一点,CD=CE,∠ACE=60°,延长BD交AE于F,连接CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y=$\frac{1}{2}$x2+x+c与x轴交于A,B的两点,与y轴交于点C,顶点为P,其中点A的坐标是(1,0).
已知抛物线y=$\frac{1}{2}$x2+x+c与x轴交于A,B的两点,与y轴交于点C,顶点为P,其中点A的坐标是(1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=x2-2x-3与坐标轴交于A、B、C三点,过y轴上一点M作BC的平行线交抛物线于C、H(G左H右).若点M在y轴上运动,试判断HM-GM的值是否发生变化?若不变化,求出其值;若变化,请说明理由.
如图,抛物线y=x2-2x-3与坐标轴交于A、B、C三点,过y轴上一点M作BC的平行线交抛物线于C、H(G左H右).若点M在y轴上运动,试判断HM-GM的值是否发生变化?若不变化,求出其值;若变化,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com