
 已知抛物线y=$\frac{1}{2}$x2+x+c与x轴交于A,B的两点,与y轴交于点C,顶点为P,其中点A的坐标是(1,0).
已知抛物线y=$\frac{1}{2}$x2+x+c与x轴交于A,B的两点,与y轴交于点C,顶点为P,其中点A的坐标是(1,0).分析 (1)先把A(1,0)代入y=$\frac{1}{2}$x2+x+c求出c=-$\frac{3}{2}$,得到抛物线解析式为y=$\frac{1}{2}$x2+x-$\frac{3}{2}$,再解方程$\frac{1}{2}$x2+x-$\frac{3}{2}$=0可得到B点坐标为(-3,0),计算自变量为0时的函数值可得到C点坐标为(0,-$\frac{3}{2}$);然后把解析式配成顶点式,根据二次函数的性质确定抛物线的对称轴和顶点P的坐标;
(2)利用描点法画二次函数的图象;
(3)画直线y=6,然后找出直线y=6与抛物线y=$\frac{1}{2}$x2+x+c的交点的坐标,则交点的横坐标即为一元二次方程$\frac{1}{2}$x2+x+c=6的解.
解答 解:(1)把A(1,0)代入y=$\frac{1}{2}$x2+x+c得$\frac{1}{2}$+1+c=0,解得c=-$\frac{3}{2}$,
所以抛物线解析式为y=$\frac{1}{2}$x2+x-$\frac{3}{2}$,
当y=0时,$\frac{1}{2}$x2+x-$\frac{3}{2}$=0,解得x1=-3,x2=1,则B点坐标为(-3,0),
当x=0时,y=$\frac{1}{2}$x2+x-$\frac{3}{2}$=y=-$\frac{3}{2}$,则C点坐标为(0,-$\frac{3}{2}$);
因为y=$\frac{1}{2}$x2+x-$\frac{3}{2}$=$\frac{1}{2}$(x+1)2-2,
所以抛物线的对称轴为直线x=-1,顶点P的坐标为(-1,-2);
(2)如图,
(3)一元二次方程$\frac{1}{2}$x2+x+c=6的解为x1=-5,x2=3.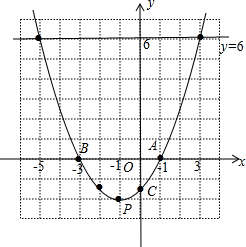
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.解决(3)的关键是找出直线y=6与抛物线的交点.


科目:初中数学 来源: 题型:选择题
 如图,两块直角三角板的直顶角O重合在一起,若∠BOC=$\frac{1}{5}$∠AOD,则∠BOC的度数为( )
如图,两块直角三角板的直顶角O重合在一起,若∠BOC=$\frac{1}{5}$∠AOD,则∠BOC的度数为( )| A. | 30° | B. | 45° | C. | 54° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=$\frac{1}{2}$BD,DF⊥AB于F.求证:CD=DF.
如图,在△ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=$\frac{1}{2}$BD,DF⊥AB于F.求证:CD=DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,等边△ABC的边长为12cm,D为AC边上一动点,E为AB延长线上一动点,DE交CB于P,点P为DE中点.
如图,等边△ABC的边长为12cm,D为AC边上一动点,E为AB延长线上一动点,DE交CB于P,点P为DE中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
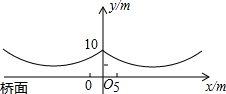 如图所示,桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,左边的一条抛物线可以用y=$\frac{9}{400}$x2+$\frac{9}{10}$x+10表示,而且左、右两条抛物线关于y轴对称.
如图所示,桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,左边的一条抛物线可以用y=$\frac{9}{400}$x2+$\frac{9}{10}$x+10表示,而且左、右两条抛物线关于y轴对称.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两个负数,绝对值大的反而小 | |
| B. | 两数之差为负,则这两数异号 | |
| C. | 任何数与零相加,都得零 | |
| D. | 正数的任何次幂都是正数;负数的偶次幂是负数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com