
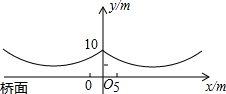
 如图所示,桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,左边的一条抛物线可以用y=$\frac{9}{400}$x2+$\frac{9}{10}$x+10表示,而且左、右两条抛物线关于y轴对称.
如图所示,桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,左边的一条抛物线可以用y=$\frac{9}{400}$x2+$\frac{9}{10}$x+10表示,而且左、右两条抛物线关于y轴对称.分析 (1)根据抛物线顶点的坐标公式可以求得顶点的横坐标和纵坐标,根据抛物线顶点的纵坐标可得出钢缆的最低点到桥面的距离;
(2)根据两最低点的横坐标可得出两条钢缆最低点之间的距离;
(3)根据左右两侧的抛物线关于y轴对称,可知两个抛物线的解析式,纵坐标相同,横坐标互为相反数,从而可以得到右侧抛物线的解析式.
解答 解:(1)∵y=$\frac{9}{400}$x2+$\frac{9}{10}$x+10,
∴该抛物线的顶点的横坐标为:x=$\frac{\frac{9}{10}}{-2×\frac{9}{400}}=-20$,纵坐标为:y=$\frac{4×\frac{9}{400}×10-(\frac{9}{10})^{2}}{4×\frac{9}{400}}=1$,
即钢缆的最低点到桥面的距离是1m;
(2)∵桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,左边的一条抛物线可以用y=$\frac{9}{400}$x2+$\frac{9}{10}$x+10表示,而且左、右两条抛物线关于y轴对称,
∴两条钢缆的顶点横坐标为,-20,20,
即两条钢缆最低点对应的横坐标分别是:-20,20,
故两条钢缆最低点之间的距离是:20-(-20)=40(米),
即两条钢缆最低点之间的距离是:40米;
(3)∵桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,左边的一条抛物线可以用y=$\frac{9}{400}$x2+$\frac{9}{10}$x+10表示,而且左、右两条抛物线关于y轴对称,
∴右侧抛物线的解析式为:y=$\frac{9}{400}{x}^{2}-\frac{9}{10}x+10$,
即抛物线右侧的表达式是:y=$\frac{9}{400}{x}^{2}-\frac{9}{10}x+10$.
点评 本题考查了二次函数的应用,解答本题的关键是掌握二次函数的顶点坐标公式,坐标和线段长度之间的转换,关于y轴对称的点和抛物线的关系.


科目:初中数学 来源: 题型:解答题
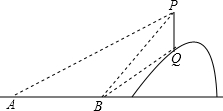 如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是26.6°,向前走30米到达B点,测得杆顶端点P和杆底端点Q的仰角分别是45°和33.7°,求该电线杆PQ的高度(结果精确到1米)
如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是26.6°,向前走30米到达B点,测得杆顶端点P和杆底端点Q的仰角分别是45°和33.7°,求该电线杆PQ的高度(结果精确到1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y=$\frac{1}{2}$x2+x+c与x轴交于A,B的两点,与y轴交于点C,顶点为P,其中点A的坐标是(1,0).
已知抛物线y=$\frac{1}{2}$x2+x+c与x轴交于A,B的两点,与y轴交于点C,顶点为P,其中点A的坐标是(1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=x2-2x-3与坐标轴交于A、B、C三点,过y轴上一点M作BC的平行线交抛物线于C、H(G左H右).若点M在y轴上运动,试判断HM-GM的值是否发生变化?若不变化,求出其值;若变化,请说明理由.
如图,抛物线y=x2-2x-3与坐标轴交于A、B、C三点,过y轴上一点M作BC的平行线交抛物线于C、H(G左H右).若点M在y轴上运动,试判断HM-GM的值是否发生变化?若不变化,求出其值;若变化,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
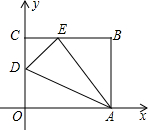 如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,
如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com