
 如图,抛物线y=x2-2x-3与坐标轴交于A、B、C三点,过y轴上一点M作BC的平行线交抛物线于C、H(G左H右).若点M在y轴上运动,试判断HM-GM的值是否发生变化?若不变化,求出其值;若变化,请说明理由.
如图,抛物线y=x2-2x-3与坐标轴交于A、B、C三点,过y轴上一点M作BC的平行线交抛物线于C、H(G左H右).若点M在y轴上运动,试判断HM-GM的值是否发生变化?若不变化,求出其值;若变化,请说明理由. 分析 作HE⊥y轴于E,GF⊥y轴于F,如图,先解方程x2-2x-3=0得到A(-1,0),B(3,0),计算自变量为0时的函数值得到C(0,-3),则△OBC为等腰直角三角形,再利用GH∥BC判断△GMF和△EMH都为等腰直角三角形,所以HM=$\sqrt{2}$HE,GM=$\sqrt{2}$GF,则HM-GM=$\sqrt{2}$(HE-GF),易得直线BC的解析式为y=x-3,可设直线GH的解析式为y=x+k,利用二次函数图象与直线的交点问题,若设H、G点的横坐标分别为a、b,则a、b为方程x2-2x-3=x+k的两根,根据根与系数的关系得到a+b=3,而HE=a,GF=-b,HM-GM=$\sqrt{2}$(HE-GF)=$\sqrt{2}$(a+b)=3$\sqrt{2}$,即HM-GM的值不发生变化.
解答 解:HM-GM的值不发生变化.
作HE⊥y轴于E,GF⊥y轴于F,如图,
当y=0时,x2-2x-3=0,解得x1=-1,x2=3,则A(-1,0),B(3,0),
当x=0时,y=x2-2x-3=-3,则C(0,-3),
∵OB=OC=3,
∴△OBC为等腰直角三角形,
∴∠OCB=45°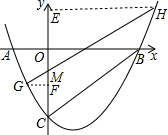
∵GH∥BC,
∴∠GMF=∠EMH=45°,
∴△GMF和△EMH都为等腰直角三角形,
∴HM=$\sqrt{2}$HE,GM=$\sqrt{2}$GF,
∴HM-GM=$\sqrt{2}$(HE-GF),
易得直线BC的解析式为y=x-3,由于GH∥BC,则可设直线GH的解析式为y=x+k,
设H、G点的横坐标分别为a、b,则a、b为方程x2-2x-3=x+k的两根,
方程整理为x2-3x-3-k=0,
∴a+b=3,
∵HE=a,GF=-b,
∴HM-GM=$\sqrt{2}$(HE-GF)=$\sqrt{2}$(a+b)=3$\sqrt{2}$,
即HM-GM的值不发生变化.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.解决本题的关键把HM-GM的值转化为点H与点G的横坐标和的$\sqrt{2}$倍.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图.已知点B、C、D在同一条直线上.△ABC和△CDE都是等边三角形,BE交AC于F,AD交CE于H,
如图.已知点B、C、D在同一条直线上.△ABC和△CDE都是等边三角形,BE交AC于F,AD交CE于H,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
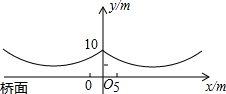 如图所示,桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,左边的一条抛物线可以用y=$\frac{9}{400}$x2+$\frac{9}{10}$x+10表示,而且左、右两条抛物线关于y轴对称.
如图所示,桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,左边的一条抛物线可以用y=$\frac{9}{400}$x2+$\frac{9}{10}$x+10表示,而且左、右两条抛物线关于y轴对称.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com