
分析 (1)按照完美点概念,求出m、n的值,代入验算,发现符合m,n是正实数,且满足m+n=mn,进而证明点(3,2)是完美点;
(2)首先根据条件求出点B的坐标,在平面直角坐标系中画出图形,利用割补法求出图形面积.
解答 解:(1)点(3,2)是完美点.
假设点(3,2)是完美点,
则:$\left\{\begin{array}{l}{m=3}\\{\frac{m}{n}=2}\end{array}\right.$,
解得:m=3,n=$\frac{3}{2}$,
根据完美点定义,应该满足:
3、$\frac{3}{2}$为正实数,
3+$\frac{3}{2}$=3×$\frac{3}{2}$,
∴点(3,2)是完美点.
(2)将点A(1,6)代入y=-x+b,
得b=7,
则直线解析式为:y=-x+7,
设点B坐标为(x,y),
∵点B满足直线y=-x+7,
∴B(x,-x+7),
∵点B是“完美点”,
∴$\left\{\begin{array}{l}{m=x}\\{\frac{m}{n}=-x+7}\end{array}\right.$ ①
∵m+n=mn,m,n是正实数,
∴$\frac{m}{n}+1=m$,②
将②代入①得:
$\left\{\begin{array}{l}{m=x}\\{m-1=-x+7}\end{array}\right.$
解得x=4,
∴点B坐标为(4,3),
在平面直角坐标系画图,如下图:
过点A做AE⊥y轴,EF⊥y轴,垂足为点E、F,
则:AE=1,BF=4,OF=EF=3,
则,S△OAB=S四边形EABO-S△OAE
=S梯形AEFB+S△OBF-S△OAE
=$\frac{1}{2}$(AE+BF)×EF+$\frac{1}{2}$×OF×BF-$\frac{1}{2}$×AE×OE,
=$\frac{1}{2}$(1+4)×3+$\frac{1}{2}$×3×4-$\frac{1}{2}$×1×6,
=$\frac{15}{2}$+6-3
=$\frac{21}{2}$.
答:△OAB的面积为$\frac{21}{2}$.
点评 题目考查了完美点的新定义及应用和平面直角坐标系中图形面积求解,题目设计新颖,既考查学生理解能力,又考查学生利用所学知识解决平面直角坐标系图形面积求解问题.


科目:初中数学 来源: 题型:解答题
 如图,已知等边三角形ABC,D为AC上一点,CD=CE,∠ACE=60°,延长BD交AE于F,连接CF.
如图,已知等边三角形ABC,D为AC上一点,CD=CE,∠ACE=60°,延长BD交AE于F,连接CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
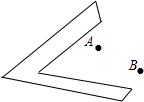 如图,在两相交公路有两村庄A、B,要修一个商店,要求到两村庄A、B的距离相等.到两公路的距离也相等.请你利用几何作图的方法,在下面的示意图中画出商店的位置.
如图,在两相交公路有两村庄A、B,要修一个商店,要求到两村庄A、B的距离相等.到两公路的距离也相等.请你利用几何作图的方法,在下面的示意图中画出商店的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=x2-2x-3与坐标轴交于A、B、C三点,过y轴上一点M作BC的平行线交抛物线于C、H(G左H右).若点M在y轴上运动,试判断HM-GM的值是否发生变化?若不变化,求出其值;若变化,请说明理由.
如图,抛物线y=x2-2x-3与坐标轴交于A、B、C三点,过y轴上一点M作BC的平行线交抛物线于C、H(G左H右).若点M在y轴上运动,试判断HM-GM的值是否发生变化?若不变化,求出其值;若变化,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com