
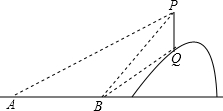
 如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是26.6°,向前走30米到达B点,测得杆顶端点P和杆底端点Q的仰角分别是45°和33.7°,求该电线杆PQ的高度(结果精确到1米)
如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是26.6°,向前走30米到达B点,测得杆顶端点P和杆底端点Q的仰角分别是45°和33.7°,求该电线杆PQ的高度(结果精确到1米)分析 延长PQ交直线AB于点E,设PE=x米,在直角△APE和直角△BPE中,根据三角函数利用x表示出AE和BE,根据AB=AE-BE即可列出方程求得x的值,再在直角△BQE中利用三角函数求得QE的长,则PQ的长度即可求解.
解答 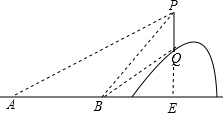 解:延长PQ交直线AB于点E,设PE=x米.
解:延长PQ交直线AB于点E,设PE=x米.
在直角△ABE中,∠PBE=45°,
则BE=PE=x米;
∵∠PAE=26.6°
在直角△APE中,AE=PE•cot∠PAE≈2x,
∵AB=AE-BE=30米,
则2x-x=30,
解得:x=30.
则BE=PE=30米.
在直角△BEQ中,QE=BE•tan∠QBE=30×tan33.7°=30×0.67≈20.1米.
∴PQ=PE-QE=30-20=10(米).
答:电线杆PQ的高度是10米.
点评 本题考查解直角三角形的应用,注意掌握当两个直角三角形有公共边时,先求出这条公共边的长是解答此类题的一般思路.


科目:初中数学 来源: 题型:选择题
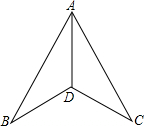 如图,在下列条件中,不能证明△ABD≌△ACD的是( )
如图,在下列条件中,不能证明△ABD≌△ACD的是( )| A. | BD=DC,AB=AC | B. | ∠ADB=∠ADC,AB=AC | C. | ∠B=∠C,∠BAD=∠CAD | D. | ∠ADB=∠ADC,BD=CD |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,两块直角三角板的直顶角O重合在一起,若∠BOC=$\frac{1}{5}$∠AOD,则∠BOC的度数为( )
如图,两块直角三角板的直顶角O重合在一起,若∠BOC=$\frac{1}{5}$∠AOD,则∠BOC的度数为( )| A. | 30° | B. | 45° | C. | 54° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
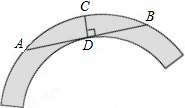 如图是一个圆环形黄花梨木摆件的残片,为求其外圆半径,小林在外圆上任取一点A,然后过点A作AB与残片的内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=15cm,AB=60cm,则这个摆件的外圆半径是37.5cm.
如图是一个圆环形黄花梨木摆件的残片,为求其外圆半径,小林在外圆上任取一点A,然后过点A作AB与残片的内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=15cm,AB=60cm,则这个摆件的外圆半径是37.5cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=$\frac{1}{2}$BD,DF⊥AB于F.求证:CD=DF.
如图,在△ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=$\frac{1}{2}$BD,DF⊥AB于F.求证:CD=DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
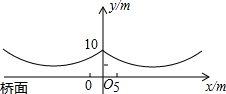 如图所示,桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,左边的一条抛物线可以用y=$\frac{9}{400}$x2+$\frac{9}{10}$x+10表示,而且左、右两条抛物线关于y轴对称.
如图所示,桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,左边的一条抛物线可以用y=$\frac{9}{400}$x2+$\frac{9}{10}$x+10表示,而且左、右两条抛物线关于y轴对称.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com