
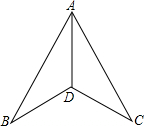
 如图,在下列条件中,不能证明△ABD≌△ACD的是( )
如图,在下列条件中,不能证明△ABD≌△ACD的是( )| A. | BD=DC,AB=AC | B. | ∠ADB=∠ADC,AB=AC | C. | ∠B=∠C,∠BAD=∠CAD | D. | ∠ADB=∠ADC,BD=CD |
分析 根据全等三角形的判定方法SSS、SAS、ASA、AAS分别进行分析即可.
解答 解:A、BD=DC,AB=AC,再加公共边AD=AD可利用SSS定理进行判定,故此选项不合题意;
B、∠ADB=∠ADC,AB=AC,再加公共边AD=AD不能判定△ABD≌△ACD,故此选项符合题意;
C、∠B=∠C,∠BAD=∠CAD再加公共边AD=AD可利用AAS定理进行判定,故此选项不合题意;
D、∠ADB=∠ADC,BD=CD再加公共边AD=AD可利用SAS定理进行判定,故此选项不合题意;
故选:B.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
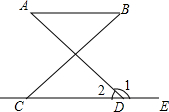 在下列推理过程中的括号里填上推理的依据.
在下列推理过程中的括号里填上推理的依据.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 我国南宋数学家杨辉所著的《详解九章算术》一书中用如图解释了二项和的乘方规律,这个图给出了(a+b)n(其中n=1,2,3,4,…)的展开式的系数规律,请根据这个规律写出(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5.
我国南宋数学家杨辉所著的《详解九章算术》一书中用如图解释了二项和的乘方规律,这个图给出了(a+b)n(其中n=1,2,3,4,…)的展开式的系数规律,请根据这个规律写出(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
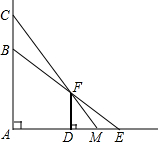 如图,一只猫头鹰蹲在树AC上的B处,通过墙顶F发现一只老鼠在E处,刚想起飞捕捉时,老鼠突然跑到矮墙DF的阴影下,猫头鹰立即从B处向上飞至树上C处时,恰巧可以通过墙顶F看到老鼠躲在M处(A、D、M、E四点在同一条直线上).
如图,一只猫头鹰蹲在树AC上的B处,通过墙顶F发现一只老鼠在E处,刚想起飞捕捉时,老鼠突然跑到矮墙DF的阴影下,猫头鹰立即从B处向上飞至树上C处时,恰巧可以通过墙顶F看到老鼠躲在M处(A、D、M、E四点在同一条直线上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
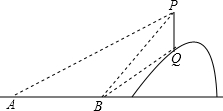 如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是26.6°,向前走30米到达B点,测得杆顶端点P和杆底端点Q的仰角分别是45°和33.7°,求该电线杆PQ的高度(结果精确到1米)
如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是26.6°,向前走30米到达B点,测得杆顶端点P和杆底端点Q的仰角分别是45°和33.7°,求该电线杆PQ的高度(结果精确到1米)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com