练习册

  • 练习册
  • 试题
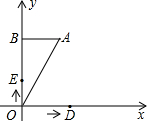    精英家教网 > 初中数学 > 题目详情

    如图，图中有一个正方形，此正方形的面积是


    1. A.
      16
    2. B.
      8
    3. C.
      4
    4. D.
      2
    B
    分析：设出正方形的边长，由勾股定理求得直角三角形的另一直角边，即正方形边长，进而求出正方形的面积．
    解答：设正方形边长为x，则x2+x2=16，于是x2=8，故正方形面积为8．故选B．
    点评：考查了正方形面积的计算，以及勾股定理的应用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    在平面直角坐标系中，放置一个如图所示的直角三角形纸片AOB，已知OA=2，∠AOB=30度．D、E两点同时从原点O出发，D点以每秒
    		3
    个单位长度的速度沿x轴正方向运动，E点以每秒1个单位精英家教网长度的速度沿y轴正方向运动，设D、E两点的运动时间为t秒．
    （1）点A的坐标为
     
    ，点B的坐标为
     
    ；
    （2）在点D、E的运动过程中，直线DE与直线OA垂直吗？请说明理由；
    （3）当时间t在什么范围时，直线DE与线段OA有公共点？
    （4）将直角三角形纸片AOB在直线DE下方的部分沿DE向上折叠，设折叠后重叠部分面积为S，请写出S与t的函数关系式，并求出S的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

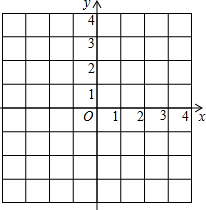    如图，平面直角坐标系中的方格阵表示一个纵横交错的街道模型的一部分，以O为原点，建立如图所示的平面直角坐标系，x轴，y轴的正方向分别表示正东、正北方向，出租车只能沿街道（网格线）行驶，且从一个路口（格点）到另一个路口，必须选择最短路线，称最短路线的长度为两个街区之间的“出租车距离”．设图中每个小正方形方格的边长为1个单位．可以发现：
    从原点O到（2，-1）的“出租车距离”为3，最短路线有3条；
    从原点O到（2，2）的“出租车距离”为4，最短路线有6条．
    （1）①从原点O到（6，1）的“出租车距离”为
    7
    7
    ．最短路线有
    7
    7
    条；
    ②与原点O的“出租车距离”等于30的路口共有
    120
    120
    个．
    （2）①解释应用：从原点O到坐标（n，2）（n为大于2的整数）的路口A，有多少条最短路线？（请给出适当的说理或过程）
    ②解决问题：
    从坐标为（1，-2）的路口到坐标为（3，36）的路口，最短路线有
    780
    780
    条．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在平面直角坐标系中，有一条直线l：与x轴、y轴分别交于点M、N，一个高为3的等边三角形ABC，边BC在x轴上，将此三角形沿着x轴的正方向平移．

    （1）在平移过程中，得到△A1B1C1，此时顶点A1恰落在直线l上，写出A1点的坐标　    　；

    （2）继续向右平移，得到△A2B2C2，此时它的外心P恰好落在直线l上，求P点的坐标；

    （3）在直线l上是否存在这样的点，与（2）中的A2、B2、C2任意两点能同时构成三个等腰三角形？如果存在，求出点的坐标；如果不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年江西省抚州市临川区罗湖中学九年级（上）第三次月考数学试卷（解析版） 题型：填空题

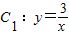    如图，把双曲线（虚线部分）沿x轴的正方向、向右平移2个单位，得一个新的双曲线C2（实线部分），对于新的双曲线C2，下列结论：
    ①双曲线C2是中心对称图形，其对称中心是（2，0）．
    ②双曲线C2仍是轴对称图形，它有两条对称轴．
    ③双曲线C2与y轴有交点，与x轴也有交点．
    ④当x＜2时，双曲线C2中的一支，y的值随着x值的增大而减小．
    其中正确结论的序号是    ．（多填或错填得0分，少填则酌情给分．）

    查看答案和解析>>

    科目：初中数学 来源：2011年江西省中考数学模拟试卷（B）（解析版） 题型：填空题

    如图，把双曲线（虚线部分）沿x轴的正方向、向右平移2个单位，得一个新的双曲线C2（实线部分），对于新的双曲线C2，下列结论：
    ①双曲线C2是中心对称图形，其对称中心是（2，0）．
    ②双曲线C2仍是轴对称图形，它有两条对称轴．
    ③双曲线C2与y轴有交点，与x轴也有交点．
    ④当x＜2时，双曲线C2中的一支，y的值随着x值的增大而减小．
    其中正确结论的序号是    ．（多填或错填得0分，少填则酌情给分．）

    查看答案和解析>>

    同步练习册答案