
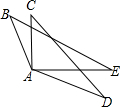
 如图,AB=AC,AE=AD,要使△ACD≌△ABE,需要补充的一个条件是( )
如图,AB=AC,AE=AD,要使△ACD≌△ABE,需要补充的一个条件是( )| A. | ∠B=∠C | B. | ∠D=∠E | C. | ∠BAC=∠EAD | D. | ∠B=∠E |
分析 只有选项C条件符合,先求出∠BAE=∠CAD,根据SAS推出两三角形全等即可.
解答 解:∠BAC=∠EAD,
理由是:∵∠BAC=∠EAD,
∴∠BAC+∠CAE=∠EAD+∠CAE,
∴∠BAE=∠CAD,
在△ACD和△ABE中,
$\left\{\begin{array}{l}{AC=AB}\\{∠CAD=∠BAE}\\{AD=AE}\end{array}\right.$,
∴△ACD≌△ABE(SAS),
选项A、选项B,选项D的条件都不能推出△ACD≌△ABE,只有选项C的条件能推出△ACD≌△ABE,
故选C.
点评 本题考查了全等三角形的判定定理的应用,能正确运用定理进行推理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.


科目:初中数学 来源:2017届江苏省盐都市九年级下学期第一次学情调研数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系xoy中,直线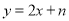 与
与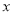 轴、
轴、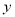 轴分别交于点A、B,与双曲线
轴分别交于点A、B,与双曲线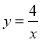 在第一象限内交于点C(1,m).
在第一象限内交于点C(1,m).
(1)求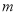 和
和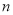 的值;
的值;
(2)过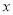 轴上的点D(
轴上的点D(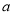 ,0)作平行于y轴的直线
,0)作平行于y轴的直线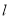 (
(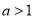 ),分别与直线AB和双曲线
),分别与直线AB和双曲线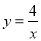 交于点P、Q,且PQ=2QD,求△APQ的面积.
交于点P、Q,且PQ=2QD,求△APQ的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
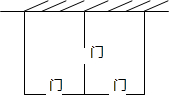 某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为( )
某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为( )| A. | 75m2 | B. | $\frac{75}{2}{m}^{2}$ | C. | 48m2 | D. | $\frac{225}{2}{m}^{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com