
ЗжЮі ЃЈ1ЃЉИљОнГЫЗНЕФвтвхЃЌНсКЯР§ЬтЃЌМДПЩЕУГіНсТлЃЛЃЈ2ЃЉИљОнГЫЗНЕФвтвхЃЌНсКЯР§ЬтЃЌМДПЩЕУГіНсТлЃЛЃЈ3ЃЉИљОнГЫЗНЕФвтвхЃЌНсКЯР§ЬтЃЌМДПЩЕУГіНсТлЃЛЃЈ4ЃЉИљОнГЫЗНЕФвтвхЃЌПЩжЊxm+n=xm•xnЃЌЬзШыЪ§ОнЃЌМДПЩЕУГіНсТлЃЎ
НтД№ НтЃКЃЈ1ЃЉ53ЁС52=ЃЈ5ЁС5ЁС5ЃЉЁСЃЈ5ЁС5ЃЉ=55ЃЎ
ЙЪД№АИЮЊЃК5ЃЎ
ЃЈ2ЃЉa3•a4=ЃЈa•a•aЃЉ•ЃЈa•a•a•aЃЉ=a7ЃЎ
ЙЪД№АИЮЊЃКЃЈa•a•aЃЉ•ЃЈa•a•a•aЃЉЃЛ7ЃЎ
ЃЈ3ЃЉЙщФЩЁЂИХРЈЃКam•an=ЃЈ$\underset{\underbrace{aЃЎaЁa}}{mИі}$ЃЉЃЈ$\underset{\underbrace{aЃЎaЁa}}{nИі}$ЃЉ=$\underset{\underbrace{aЃЎaЃЎaЁa}}{ЃЈm+nЃЉИі}$=am+nЃЎ
ЙЪД№АИЮЊЃКm+nЃЎ
ЃЈ4ЃЉxm+n=xm•xn=4ЁС5=20ЃЎ
ЙЪД№АИЮЊЃК20ЃЎ
ЕуЦР БОЬтПМВщСЫгаРэЪ§ЕФГЫЗЈЃЌНтЬтЕФЙиМќЪЧЃКЖСЖЎГЫЗНЕФвтвхЃЌВЂФмЗТееР§ЬтНтОіЪЕР§ЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 ШчЭМЃЌЕуOЪЧЕШБпЁїABCФквЛЕуЃЎЁЯCOB=140ЁуЃЌЁЯAOB=ІСЃЌНЋЁїCOBШЦЕуCАДЫГЪБеыЗНЯђа§зЊ60ЁуЕУЁїADCЃЌСЌНгOD
ШчЭМЃЌЕуOЪЧЕШБпЁїABCФквЛЕуЃЎЁЯCOB=140ЁуЃЌЁЯAOB=ІСЃЌНЋЁїCOBШЦЕуCАДЫГЪБеыЗНЯђа§зЊ60ЁуЕУЁїADCЃЌСЌНгODВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
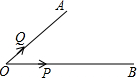 ШчЭМЃЌдкЁЯAOB=30ЁуЕФСНБпЩЯгаСНЕуPКЭQдкдЫЖЏЃЌЧвЕуPДгРыЕуOга1РхУздЖЕФЕиЗНГіЗЂЃЌвд1РхУзУПУыдЫЖЏЃЌЕуQДгЕуOГіЗЂвд2РхУзУПУыдЫЖЏЃЌдђЁїPOQЮЊЕШбќШ§НЧаЮЪБЃЌСНЕуЕФдЫЖЏЪБМфЮЊЃЈЁЁЁЁЃЉУыЃЎ
ШчЭМЃЌдкЁЯAOB=30ЁуЕФСНБпЩЯгаСНЕуPКЭQдкдЫЖЏЃЌЧвЕуPДгРыЕуOга1РхУздЖЕФЕиЗНГіЗЂЃЌвд1РхУзУПУыдЫЖЏЃЌЕуQДгЕуOГіЗЂвд2РхУзУПУыдЫЖЏЃЌдђЁїPOQЮЊЕШбќШ§НЧаЮЪБЃЌСНЕуЕФдЫЖЏЪБМфЮЊЃЈЁЁЁЁЃЉУыЃЎ| AЃЎ | $1ЃЛ2\sqrt{3}+3ЃЛ\frac{{2\sqrt{3}+1}}{11}$ | BЃЎ | $1ЃЛ2\sqrt{3}+3ЃЛ\frac{{2\sqrt{3}+1}}{13}$ | CЃЎ | $1ЃЛ2\sqrt{3}+3$ЃЛ5 | DЃЎ | вдЩЯЖМВЛЖд |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
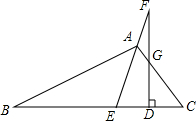 ШчЭМЃЌдкЁїABCжаЃЌAEЪЧЁїABCЕФНЧЦНЗжЯпЃЌдкEAЕФбгГЄЯпЩЯШЁвЛЕуFЃЌзїFDЁЭBCгкЕуDЃЌШєЁЯB=36ЁуЃЌЁЯC=64ЁуЃЌдђЁЯEFDЕФЖШЪ§ЮЊЃЈЁЁЁЁЃЉ
ШчЭМЃЌдкЁїABCжаЃЌAEЪЧЁїABCЕФНЧЦНЗжЯпЃЌдкEAЕФбгГЄЯпЩЯШЁвЛЕуFЃЌзїFDЁЭBCгкЕуDЃЌШєЁЯB=36ЁуЃЌЁЯC=64ЁуЃЌдђЁЯEFDЕФЖШЪ§ЮЊЃЈЁЁЁЁЃЉ| AЃЎ | 10Ёу | BЃЎ | 12Ёу | CЃЎ | 14Ёу | DЃЎ | 16Ёу |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com