
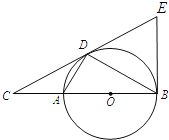
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,若BC=4,tan∠ABD=![]() ,求BE的长.
,求BE的长.
【答案】(1)证明见解析;(2)3.
【解析】
(1)连OD,OE,根据圆周角定理得到∠ADO+∠1=90°,而∠CDA=∠CBD,∠CBD=∠1,于是∠CDA+∠ADO=90°;
(2)根据切线的性质得到ED=EB,OE⊥BD,则∠ABD=∠OEB,得到tan∠CDA=tan∠OEB=![]() =
=![]() ,易证Rt△CDO∽Rt△CBE,得到
,易证Rt△CDO∽Rt△CBE,得到![]() =
=![]() =
=![]() =
=![]() ,求得CD,然后在Rt△CBE中,运用勾股定理可计算出BE的长.
,求得CD,然后在Rt△CBE中,运用勾股定理可计算出BE的长.
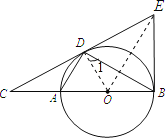
(1)连OD,OE,如图,
∵AB为直径,
∴∠ADB=90°,即∠ADO+∠1=90°,
又∵∠CDA=∠CBD,
而∠CBD=∠1,
∴∠1=∠CDA,
∴∠CDA+∠ADO=90°,即∠CDO=90°,
∴CD是⊙O的切线;
(2)解:∵EB为⊙O的切线,
∴ED=EB,OE⊥DB,
∴∠ABD+∠DBE=90°,∠OEB+∠DBE=90°,
∴∠ABD=∠OEB,
∴∠CDA=∠OEB.
而tan∠ABD=![]() ,
,
∴tan∠CDA=![]() ,
,
∴tan∠OEB=![]() =
=![]() ,
,
∵Rt△CDO∽Rt△CBE,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴CD=![]() ×4=2,
×4=2,
在Rt△CBE中,设BE=x,
∴(x+2)2=x2+42,
解得x=3.
即BE的长为3.


科目:初中数学 来源: 题型:
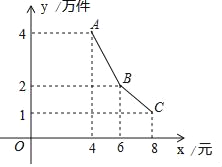
【题目】为了支持大学生创业,某市政府出台了一项优惠政策:提供10万元的无息创业贷款.小王利用这笔贷款,注册了一家淘宝网店,招收5名员工,销售一种火爆的电子产品,并约定用该网店经营的利润,逐月偿还这笔无息贷款.已知该产品的成本为每件4元,员工每人每月的工资为4千元,该网店还需每月支付其它费用1万元.该产品每月销售量y(万件)与销售单价x(元)万件之间的函数关系如图所示.
(1)求该网店每月利润w(万元)与销售单价x(元)之间的函数表达式;
(2)小王自网店开业起,最快在第几个月可还清10万元的无息贷款?
查看答案和解析>>
科目:初中数学 来源: 题型:
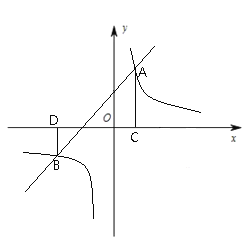
【题目】综合与探究:
如图所示,在平面直角坐标系中,直线![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() .
.
(1)求![]() ,
,![]() 的值及反比例函数的函数表达式;
的值及反比例函数的函数表达式;
(2)若点![]() 在线段
在线段![]() 上,且
上,且![]() ,请求出此时点
,请求出此时点![]() 的坐标;
的坐标;
(3)小颖在探索中发现:在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰三角形.请你直接写出点
为顶角的等腰三角形.请你直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市大力发展乡村旅游产业,全力打造客都美丽乡村”,其中“客家美景、客家文化、客家美食”享誉全省,游人络绎不绝.去年我市某村村民抓住机遇,投入20万元创办农家乐(餐饮+住宿),一年时间就收回投资的80%,其中餐饮收入是住宿收入的2倍还多1万元.
(1)求去年该农家乐餐饮和住宿的收入各为多少万元?
(2)今年该村村民再投入了10万元,增设了土特产的实体销售和网上销售项目并实现盈利,村民在接受记者采访时说,预计今年餐饮和住宿的收入比去年还会有10%的增长.这两年的总收入除去所有投资外还能获得不少于10万元的纯利润,请问今年土特产销售至少收入多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
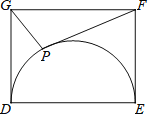
【题目】在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )
A. ![]() B.
B. ![]() C. 34 D. 10
C. 34 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )

A. 2 B. 3 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数![]() 的图像与边长是6的正方形
的图像与边长是6的正方形![]() 的两边
的两边![]() ,
,![]() 分别相交于
分别相交于![]() ,
,![]() 两点.
两点.
(1)若点![]() 是
是![]() 边的中点,求反比例函数
边的中点,求反比例函数![]() 的解析式和点
的解析式和点![]() 的坐标;
的坐标;
(2)若![]() ,求直线
,求直线![]() 的解析式及
的解析式及![]() 的面积
的面积

查看答案和解析>>
科目:初中数学 来源: 题型:
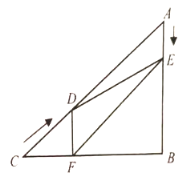
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;同时,动点
;同时,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;当一个点停止运动,另一个点也停止运动.设点
;当一个点停止运动,另一个点也停止运动.设点![]() ,
,![]() 运动的时间是
运动的时间是![]()
![]()
![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)![]() 为何值时,
为何值时,![]() ?
?
(2)设四边形![]() 的面积为
的面积为![]() ,试求出
,试求出![]() 与
与![]() 之间的关系式;
之间的关系式;
(3)是否存在某一时刻![]() ,使得
,使得![]() 若存在,求出
若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(4)当![]() 为何值时,
为何值时,![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
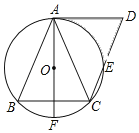
【题目】如图,AB=AC,⊙O为△ABC的外接圆,AF为⊙O的直径,四边形ABCD是平行四边形.
(1)求证:AD是⊙O的切线;
(2)若∠BAC=45°,AF=2,求阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com