
【题目】如图,在平面直角坐标系中,反比例函数![]() 的图像与边长是6的正方形
的图像与边长是6的正方形![]() 的两边
的两边![]() ,
,![]() 分别相交于
分别相交于![]() ,
,![]() 两点.
两点.
(1)若点![]() 是
是![]() 边的中点,求反比例函数
边的中点,求反比例函数![]() 的解析式和点
的解析式和点![]() 的坐标;
的坐标;
(2)若![]() ,求直线
,求直线![]() 的解析式及
的解析式及![]() 的面积
的面积

【答案】(1)![]() ,N(3,6);(2)y=-x+8,S△OMN=16.
,N(3,6);(2)y=-x+8,S△OMN=16.
【解析】
(1)求出点M坐标,利用待定系数法即可求得反比例函数的解析式,把N点的纵坐标代入解析式即可求得横坐标;
(2)根据M点的坐标与反比例函数的解析式,求得N点的坐标,利用待定系数法求得直线MN的解析式,根据△OMN=S正方形OABC-S△OAM-S△OCN-S△BMN即可得到答案.
解:(1)∵点M是AB边的中点,∴M(6,3).
∵反比例函数y=![]() 经过点M,∴3=
经过点M,∴3=![]() .∴k=18.
.∴k=18.
∴反比例函数的解析式为y=![]() .
.
当y=6时,x=3,∴N(3,6).
(2)由题意,知M(6,2),N(2,6).
设直线MN的解析式为y=ax+b,则
![]() ,
,
解得![]() ,
,
∴直线MN的解析式为y=-x+8.
∴S△OMN=S正方形OABC-S△OAM-S△OCN-S△BMN=36-6-6-8=16.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 在射线
在射线![]() 上,以
上,以![]() 为半径的
为半径的![]() 交边
交边![]() 于点
于点![]() (点
(点![]() 与点
与点![]() 不重合),联结
不重合),联结![]() 、
、![]() ,设
,设![]() ,
,![]() .
.
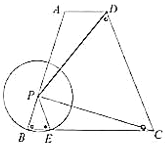
(1)求证:![]() ;
;
(2)求![]() 关于
关于![]() 的函数解析式,并写出定义域;
的函数解析式,并写出定义域;
(3)联结![]() ,当
,当![]() 时,以
时,以![]() 为圆心半径为
为圆心半径为![]() 的
的![]() 与
与![]() 相交,求
相交,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,双曲线![]() 经过矩形OABC的边BC的中点E,交AB于点D.设点B的坐标为(m,n).
经过矩形OABC的边BC的中点E,交AB于点D.设点B的坐标为(m,n).
(1)直接写出点E的坐标,并求出点D的坐标;(用含m,n的代数式表示)
(2)若梯形ODBC的面积为![]() ,求双曲线的函数解析式.
,求双曲线的函数解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由7个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
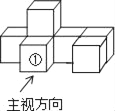
A. 主视图改变,俯视图改变 B. 左视图改变,俯视图改变
C. 俯视图不变,左视图改变 D. 主视图不变,左视图不变
查看答案和解析>>
科目:初中数学 来源: 题型:
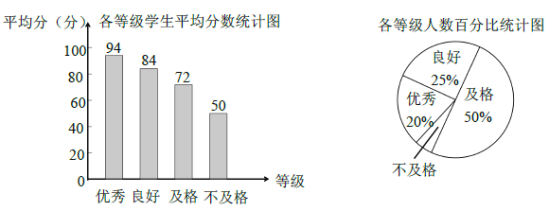
【题目】《中学生体质健康标准》规定学生体质健康等级标准为:90分及以上为优秀;80分~89分为良好;60分~79分为及格;59分及以下为不及格. 某校从九年级学生中随机抽取了![]() 的学生进行了体质测试,得分情况如下图.
的学生进行了体质测试,得分情况如下图.
(1)在抽取的学生中不及格人数所占的百分比是 ,它的圆心角度数为 度.
(2)小明按以下方法计算出抽取的学生平均得分是:![]() . 根据所学的统计知识判断小明的计算是否正确,若不正确,请计算正确结果.
. 根据所学的统计知识判断小明的计算是否正确,若不正确,请计算正确结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级数学小组在课外活动中,研究了同一坐标系中两个反比例函数![]() 与
与![]()
![]() 在第一象限图象的性质,经历了如下探究过程:
在第一象限图象的性质,经历了如下探究过程:
操作猜想:
(1)如图①,当![]() ,
,![]() 时,在
时,在![]() 轴的正方向上取一点
轴的正方向上取一点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .当
.当![]() 时,
时,![]() ________,
________,![]() ________,
________,![]() ________;当
________;当![]() 时,
时,![]() ________,
________,![]() ________,
________,![]() ________;当
________;当![]() 时,猜想
时,猜想![]() ________.
________.

数学思考:
(2)在![]() 轴的正方向上任意取点
轴的正方向上任意取点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 于点
于点![]() 、交
、交![]() 于点
于点![]() ,请用含
,请用含![]() 、
、![]() 的式子表示
的式子表示![]() 的值,并利用图②加以证明.
的值,并利用图②加以证明.

推广应用:
(3)如图③,若![]() ,
,![]() ,在
,在![]() 轴的正方向上分别取点
轴的正方向上分别取点![]() 、
、![]()
![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 于点
于点![]() 、
、![]() ,交
,交![]() 于点
于点![]() 、
、![]() ,是否存在四边形
,是否存在四边形![]() 是正方形?如果存在,求
是正方形?如果存在,求![]() 的长和点
的长和点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,对角线AC与BD交于点O,在Rt△PFE中,∠EPF=90°,点E、F分别在边AD、AB上.
(1)如图1,若点P与点O重合:①求证:AF=DE;②若正方形的边长为2![]() ,当∠DOE=15°时,求线段EF的长;
,当∠DOE=15°时,求线段EF的长;
(2)如图2,若Rt△PFE的顶点P在线段OB上移动(不与点O、B重合),当BD=3BP时,证明:PE=2PF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com