
【题目】已知:如图,梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 在射线
在射线![]() 上,以
上,以![]() 为半径的
为半径的![]() 交边
交边![]() 于点
于点![]() (点
(点![]() 与点
与点![]() 不重合),联结
不重合),联结![]() 、
、![]() ,设
,设![]() ,
,![]() .
.
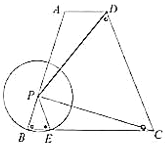
(1)求证:![]() ;
;
(2)求![]() 关于
关于![]() 的函数解析式,并写出定义域;
的函数解析式,并写出定义域;
(3)联结![]() ,当
,当![]() 时,以
时,以![]() 为圆心半径为
为圆心半径为![]() 的
的![]() 与
与![]() 相交,求
相交,求![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]()
【解析】
![]() 根据梯形的性质得到
根据梯形的性质得到![]() ,根据等腰三角形的性质得到
,根据等腰三角形的性质得到![]() ,根据平行线的判定定理即可得到结论;
,根据平行线的判定定理即可得到结论;
![]() 分别过P、A、D作BC的垂线,垂足分别为点H、F、
分别过P、A、D作BC的垂线,垂足分别为点H、F、![]() 推出四边形ADGF是矩形,
推出四边形ADGF是矩形,![]() ,求得
,求得![]() ,根据勾股定理得到
,根据勾股定理得到![]() ,根据平行线分线段成比例定理得到
,根据平行线分线段成比例定理得到![]() ,
,![]() ,求得
,求得![]() ,根据勾股定理即可得到结论;
,根据勾股定理即可得到结论;
![]() 作
作![]() 交DC于
交DC于![]() 推出四边形PDME是平行四边形
推出四边形PDME是平行四边形![]() 得到
得到![]() ,即
,即![]() ,根据相似三角形的性质得到
,根据相似三角形的性质得到![]() ,根据相切两圆的性质即可得到结论.
,根据相切两圆的性质即可得到结论.
![]() 证明:梯形ABCD,
证明:梯形ABCD,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
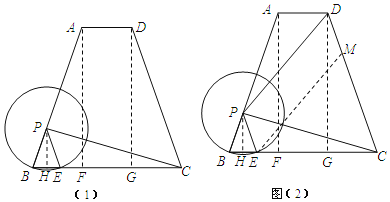
![]() 解:分别过P、A、D作BC的垂线,垂足分别为点H、F、G.
解:分别过P、A、D作BC的垂线,垂足分别为点H、F、G.
![]() 梯形ABCD中,
梯形ABCD中,![]() ,
,
,![]() ,
,![]() ,
,
![]() 四边形ADGF是矩形,
四边形ADGF是矩形,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 中,
中,
![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,即
,即![]() ,
,
![]() 解:作
解:作![]() 交DC于M.
交DC于M.
![]() ,
,
![]() 四边形PDME是平行四边形.
四边形PDME是平行四边形.
![]() ,即
,即![]() ,
,
![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
![]() .
.
![]() ∽
∽![]() ,
,
![]() ,即
,即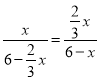 ,
,
解得:![]() ,
,
即![]() ,
,
![]() ,
,
当两圆外切时,![]() ,即
,即![]() 舍去
舍去![]() ;
;
当两圆内切时,![]() ,即
,即![]() 舍去
舍去![]() ,
,![]() ;
;
即两圆相交时,![]() .
.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把1,1,2,3,5,8,13,21,…,这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧 ![]() ,
,![]() ,
,![]() ,…,得到斐波那契螺旋线,然后顺次连结P1P2,P2P3,P3P4,…,得到螺旋折线(如图),已知点P1(0,1),P2(-1,0),P3(0,-1),则该折线上的点P9的坐标为( )
,…,得到斐波那契螺旋线,然后顺次连结P1P2,P2P3,P3P4,…,得到螺旋折线(如图),已知点P1(0,1),P2(-1,0),P3(0,-1),则该折线上的点P9的坐标为( )
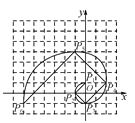
A. (-6,24)B. (-6,25)C. (-5,24)D. (-5,25)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=![]() x2+
x2+![]() x-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线l经过A,C两点,连接BC.
x-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线l经过A,C两点,连接BC.
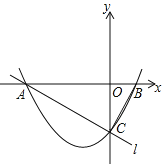
(1)求直线l的解析式;
(2)若直线x=m(m<0)与该抛物线在第三象限内交于点E,与直线l交于点D,连接OD.当OD⊥AC时,求线段DE的长;
(3)取点G(0,-1),连接AG,在第一象限内的抛物线上,是否存在点P,使∠BAP=∠BCO-∠BAG?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小丽暑期参加工厂社会实践活动,师傅将他们工作第一周每天生产的合格产品的个数整理成如表两组数据,那么关于他们工作第一周每天生产的合格产品个数,下列说法中正确的是( )
小明 | 2 | 6 | 7 | 7 | 8 |
小丽 | 2 | 3 | 4 | 8 | 8 |
A. 小明的平均数小于小丽的平均数
B. 两人的中位数相同
C. 两人的众数相同
D. 小明的方差小于小丽的方差
查看答案和解析>>
科目:初中数学 来源: 题型:
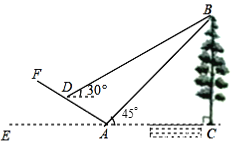
【题目】如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角是45°,沿斜坡走![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1︰2.则小明从点A走到点D的过程中,他上升的高度为____米;大树BC的高度为____米(结果保留根号).
米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1︰2.则小明从点A走到点D的过程中,他上升的高度为____米;大树BC的高度为____米(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
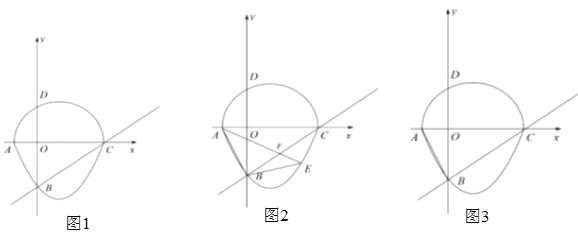
【题目】如图,我们把一个半圆和抛物线的一部分围成的封闭图形称为“果圆”,已知![]() 分别为“果圆”与坐标轴的交点,直线
分别为“果圆”与坐标轴的交点,直线![]() 与“果圆”中的抛物线
与“果圆”中的抛物线![]() 交于
交于![]() 两点
两点
(1)求“果圆”中抛物线的解析式,并直接写出“果圆”被![]() 轴截得的线段
轴截得的线段![]() 的长;
的长;
(2)如图,![]() 为直线
为直线![]() 下方“果圆”上一点,连接
下方“果圆”上一点,连接![]() ,设
,设![]() 与
与![]() 交于
交于![]() ,
,![]() 的面积记为
的面积记为![]() ,
,![]() 的面积即为
的面积即为![]() ,求
,求![]() 的最小值
的最小值
(3)“果圆”上是否存在点![]() ,使
,使![]() ,如果存在,直接写出点
,如果存在,直接写出点![]() 坐标,如果不存在,请说明理由
坐标,如果不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数![]() 的图像与边长是6的正方形
的图像与边长是6的正方形![]() 的两边
的两边![]() ,
,![]() 分别相交于
分别相交于![]() ,
,![]() 两点.
两点.
(1)若点![]() 是
是![]() 边的中点,求反比例函数
边的中点,求反比例函数![]() 的解析式和点
的解析式和点![]() 的坐标;
的坐标;
(2)若![]() ,求直线
,求直线![]() 的解析式及
的解析式及![]() 的面积
的面积

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,经过原点O的抛物线y=ax2+bx(a≠0)与x轴交于另一点A(3,0),在第一象限内与直线y=x交于点B(4,t).
(1)求这条抛物线的表达式;
(2)在直线OB下方的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积最大,求点C的坐标;
(3)如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com