
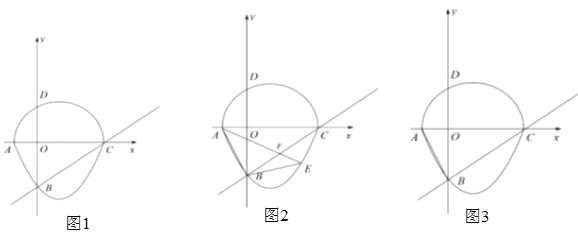
【题目】如图,我们把一个半圆和抛物线的一部分围成的封闭图形称为“果圆”,已知![]() 分别为“果圆”与坐标轴的交点,直线
分别为“果圆”与坐标轴的交点,直线![]() 与“果圆”中的抛物线
与“果圆”中的抛物线![]() 交于
交于![]() 两点
两点
(1)求“果圆”中抛物线的解析式,并直接写出“果圆”被![]() 轴截得的线段
轴截得的线段![]() 的长;
的长;
(2)如图,![]() 为直线
为直线![]() 下方“果圆”上一点,连接
下方“果圆”上一点,连接![]() ,设
,设![]() 与
与![]() 交于
交于![]() ,
,![]() 的面积记为
的面积记为![]() ,
,![]() 的面积即为
的面积即为![]() ,求
,求![]() 的最小值
的最小值
(3)“果圆”上是否存在点![]() ,使
,使![]() ,如果存在,直接写出点
,如果存在,直接写出点![]() 坐标,如果不存在,请说明理由
坐标,如果不存在,请说明理由
【答案】(1)![]() ;6;(2)
;6;(2)![]() 有最小值
有最小值![]() ;(3)
;(3)![]() ,
,![]() .
.
【解析】
(1)先求出点B,C坐标,利用待定系数法求出抛物线解析式,进而求出点A坐标,即可求出半圆的直径,再构造直角三角形求出点D的坐标即可求出BD;
(2)先判断出要求![]() 的最小值,只要CG最大即可,再求出直线EG解析式和抛物线解析式联立成的方程只有一个交点,求出直线EG解析式,即可求出CG,结论得证.
的最小值,只要CG最大即可,再求出直线EG解析式和抛物线解析式联立成的方程只有一个交点,求出直线EG解析式,即可求出CG,结论得证.
(3)求出线段AC,BC进而判断出满足条件的一个点P和点B重合,再利用抛物线的对称性求出另一个点P.
解:(1) 对于直线y=![]() x-3,令x=0,
x-3,令x=0,
∴y=-3,
∴B(0,-3),
令y=0,
∴![]() x-3=0,
x-3=0,
∴x=4,
∴C(4,0),
∵抛物线y=![]() x2+bx+c过B,C两点,
x2+bx+c过B,C两点,
∴
∴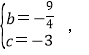
∴抛物线的解析式为y=![]() ;
;
令y=0,
∴![]() =0,
=0,
∴x=4或x=-1,
∴A(-1,0),
∴AC=5,
如图2,记半圆的圆心为O',连接O'D,

∴O'A=O'D=O'C=![]() AC=
AC=![]() ,
,
∴OO'=OC-O'C=4-![]() =
=![]() ,
,
在Rt△O'OD中,OD=![]() =2,
=2,
∴D(0,2),
∴BD=2-(-3)=5;
(2) 如图3,
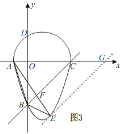
∵A(-1,0),C(4,0),
∴AC=5,
过点E作EG∥BC交x轴于G,
∵△ABF的AF边上的高和△BEF的EF边的高相等,设高为h,
∴S△ABF=![]() AFh,S△BEF=
AFh,S△BEF=![]() EFh,
EFh,
∴![]() =
=![]() =
= ![]()
∵![]() 的最小值,
的最小值,
∴![]() 最小,
最小,
∵CF∥GE,
∴![]()
∴![]() 最小,即:CG最大,
最小,即:CG最大,
∴EG和果圆的抛物线部分只有一个交点时,CG最大,
∵直线BC的解析式为y=![]() x-3,
x-3,
设直线EG的解析式为y=![]() x+m①,
x+m①,
∵抛物线的解析式为y=![]() x2-
x2-![]() x-3②,
x-3②,
联立①②化简得,3x2-12x-12-4m=0,
∴△=144+4×3×(12+4m)=0,
∴m=-6,
∴直线EG的解析式为y=![]() x-6,
x-6,
令y=0,
∴![]() x-6=0,
x-6=0,
∴x=8,
∴CG=4,
∴![]() =
=![]() ;
;
(3)![]() ,
,![]() .理由:
.理由:
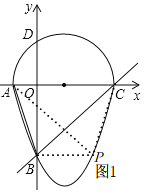
如图1
∴半圆上除点A,C外任意一点Q,都有∠AQC=90°,
∴点P只能在抛物线部分上,
∵B(0,-3),C(4,0),
∴BC=5,
∵AC=5,
∴AC=BC,
∴∠BAC=∠ABC,
当∠APC=∠CAB时,点P和点B重合,即:P(0,-3),
由抛物线的对称性知,另一个点P的坐标为(3,-3),
即:使∠APC=∠CAB,点P坐标为(0,-3)或(3,-3).


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某校开展的“好书伴我成长”课外阅读活动中,为了解八年级学生的课外阅读情况,随机抽查部分学生,并对其课外阅读量进行统计分析,绘制成图1、图2两幅尚不完整的统计图,请根据图中信息,解答下列问题:
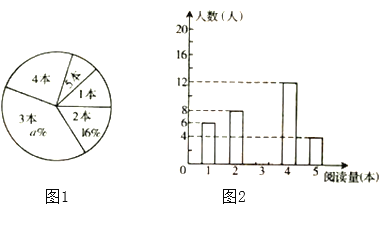
(1)求被抽查的学生人数及课外阅读量的平均数;
(2)求扇形统计图中![]() 的值;
的值;
(3)根据样本数据,估计该校八年级800名学生在本次活动中课外阅读量多于2本的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 在射线
在射线![]() 上,以
上,以![]() 为半径的
为半径的![]() 交边
交边![]() 于点
于点![]() (点
(点![]() 与点
与点![]() 不重合),联结
不重合),联结![]() 、
、![]() ,设
,设![]() ,
,![]() .
.
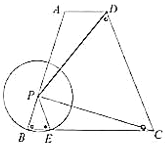
(1)求证:![]() ;
;
(2)求![]() 关于
关于![]() 的函数解析式,并写出定义域;
的函数解析式,并写出定义域;
(3)联结![]() ,当
,当![]() 时,以
时,以![]() 为圆心半径为
为圆心半径为![]() 的
的![]() 与
与![]() 相交,求
相交,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
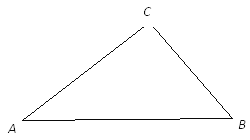
【题目】如图,已知点D、E分别在△ACD的边AB和AC上,已知DE∥BC,DE=DB.
(1)请用直尺和圆规在图中画出点D和点E(保留作图痕迹,不要求写作法),并证明所作的线段DE是符合题目要求的;
(2)若AB=7,BC=3,请求出DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,双曲线![]() 经过矩形OABC的边BC的中点E,交AB于点D.设点B的坐标为(m,n).
经过矩形OABC的边BC的中点E,交AB于点D.设点B的坐标为(m,n).
(1)直接写出点E的坐标,并求出点D的坐标;(用含m,n的代数式表示)
(2)若梯形ODBC的面积为![]() ,求双曲线的函数解析式.
,求双曲线的函数解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由7个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
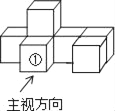
A. 主视图改变,俯视图改变 B. 左视图改变,俯视图改变
C. 俯视图不变,左视图改变 D. 主视图不变,左视图不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国科学技术馆有“圆与非圆”展品,涉及了“等宽曲线”的知识.因为圆的任何一对平行切线的距离总是相等的,所以圆是“等宽曲线”.除了例以外,还有一些几何图形也是“等宽曲线”,如勒洛只角形(图1),它是分别以等边三角形的征个顶点为圆心,以边长为半径,在另两个顶点间画一段圆弧.三段圆弧围成的曲边三角形.图2是等宽的勒洛三角形和圆.
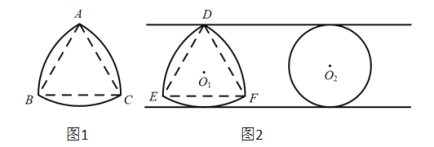
下列说法中错误的是( )
A.勒洛三角形是轴对称图形
B.图1中,点A到![]() 上任意一点的距离都相等
上任意一点的距离都相等
C.图2中,勒洛三角形上任意一点到等边三角形DEF的中心![]() 的距离都相等
的距离都相等
D.图2中,勒洛三角形的周长与圆的周长相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com