
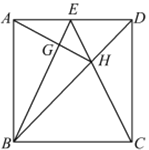
【题目】如图,正方形![]() 中,点
中,点![]() 是
是![]() 边的中点,
边的中点,![]() 交于点
交于点![]() ,
,![]() 交于点
交于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的答案是____.
,其中正确的答案是____.
【答案】①②③④
【解析】
首先根据正方形的性质证得△BAE≌△CDE,推出∠ABE=∠DCE,再证△ADH≌△CDH,求得∠HAD=∠HCD,推出∠ABE=∠HAD;求出∠ABE+∠BAG=90°;最后在△AGE中根据三角形的内角和是180°求得∠AGE=90°即可得到①正确.根据tan∠ABE=tan∠EAG=![]() ,得到AG=
,得到AG=![]() BG,GE=
BG,GE=![]() AG,于是得到BG=4EG,故②正确;根据AD∥BC,求出S△BDE=S△CDE,推出S△BDE-S△DEH=S△CDE-S△DEH,即:S△BHE=S△CHD,故③正确;由∠AHD=∠CHD,得到邻补角和对顶角相等得到∠AHB=∠EHD,故④正确;
AG,于是得到BG=4EG,故②正确;根据AD∥BC,求出S△BDE=S△CDE,推出S△BDE-S△DEH=S△CDE-S△DEH,即:S△BHE=S△CHD,故③正确;由∠AHD=∠CHD,得到邻补角和对顶角相等得到∠AHB=∠EHD,故④正确;
解:∵四边形ABCD是正方形,E是AD边上的中点,
∴AE=DE,AB=CD,∠BAD=∠CDA=90°,
∴△BAE≌△CDE(SAS),
∴∠ABE=∠DCE,
∵四边形ABCD是正方形,
∴AD=DC,∠ADB=∠CDB=45°,DH=DH,
∴△ADH≌△CDH(SAS),
∴∠HAD=∠HCD,
∵∠ABE=∠DCE
∴∠ABE=∠HAD,
∵∠BAD=∠BAH+∠DAH=90°,
∴∠ABE+∠BAH=90°,
∴∠AGB=180°-90°=90°,
∴AG⊥BE,故①正确;
∵tan∠ABE=tan∠EAG=![]() ,
,
![]() ,
,
∴BG=4EG,故②正确;
∵AD∥BC,
∴S△BDE=S△CDE,
∴S△BDE-S△DEH=S△CDE-S△DEH,
即;S△BHE=S△CHD,故③正确;
∵△ADH≌△CDH,
∴∠AHD=∠CHD,
∴∠AHB=∠CHB,
∵∠BHC=∠DHE,
∴∠AHB=∠EHD,故④正确;
故答案为①②③④.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】我们把1,1,2,3,5,8,13,21,…,这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧 ![]() ,
,![]() ,
,![]() ,…,得到斐波那契螺旋线,然后顺次连结P1P2,P2P3,P3P4,…,得到螺旋折线(如图),已知点P1(0,1),P2(-1,0),P3(0,-1),则该折线上的点P9的坐标为( )
,…,得到斐波那契螺旋线,然后顺次连结P1P2,P2P3,P3P4,…,得到螺旋折线(如图),已知点P1(0,1),P2(-1,0),P3(0,-1),则该折线上的点P9的坐标为( )
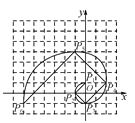
A. (-6,24)B. (-6,25)C. (-5,24)D. (-5,25)
查看答案和解析>>
科目:初中数学 来源: 题型:
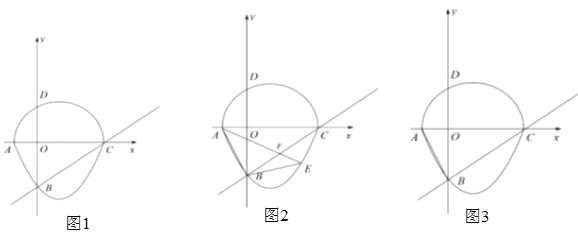
【题目】如图,我们把一个半圆和抛物线的一部分围成的封闭图形称为“果圆”,已知![]() 分别为“果圆”与坐标轴的交点,直线
分别为“果圆”与坐标轴的交点,直线![]() 与“果圆”中的抛物线
与“果圆”中的抛物线![]() 交于
交于![]() 两点
两点
(1)求“果圆”中抛物线的解析式,并直接写出“果圆”被![]() 轴截得的线段
轴截得的线段![]() 的长;
的长;
(2)如图,![]() 为直线
为直线![]() 下方“果圆”上一点,连接
下方“果圆”上一点,连接![]() ,设
,设![]() 与
与![]() 交于
交于![]() ,
,![]() 的面积记为
的面积记为![]() ,
,![]() 的面积即为
的面积即为![]() ,求
,求![]() 的最小值
的最小值
(3)“果圆”上是否存在点![]() ,使
,使![]() ,如果存在,直接写出点
,如果存在,直接写出点![]() 坐标,如果不存在,请说明理由
坐标,如果不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数![]() 的图像与边长是6的正方形
的图像与边长是6的正方形![]() 的两边
的两边![]() ,
,![]() 分别相交于
分别相交于![]() ,
,![]() 两点.
两点.
(1)若点![]() 是
是![]() 边的中点,求反比例函数
边的中点,求反比例函数![]() 的解析式和点
的解析式和点![]() 的坐标;
的坐标;
(2)若![]() ,求直线
,求直线![]() 的解析式及
的解析式及![]() 的面积
的面积

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某工厂与![]() 两地有铁路相连,该工厂从
两地有铁路相连,该工厂从![]() 地购买原材料,制成产品销往
地购买原材料,制成产品销往![]() 地. 已知每吨进价为600元(含加工费),加工过程中1吨原料可生产产品
地. 已知每吨进价为600元(含加工费),加工过程中1吨原料可生产产品![]() 吨,当预计销售产品不超过120吨时,每吨售价1600元,超过120吨,每增加1吨,销售所有产品的价格降低2元. 设该工厂有
吨,当预计销售产品不超过120吨时,每吨售价1600元,超过120吨,每增加1吨,销售所有产品的价格降低2元. 设该工厂有![]() 吨产品销往
吨产品销往![]() 地. (利润=售价—进价—运费)
地. (利润=售价—进价—运费)
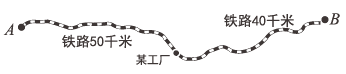

(1)用![]() 的代数式表示购买的原材料有 吨.
的代数式表示购买的原材料有 吨.
(2)从![]() 地购买原材料并加工制成产品销往
地购买原材料并加工制成产品销往![]() 地后,若总运费为9600元,求
地后,若总运费为9600元,求![]() 的值,并直接写出这批产品全部销售后的总利润.
的值,并直接写出这批产品全部销售后的总利润.
(3)现工厂销往![]() 地的产品至少120吨,且每吨售价不得低于1440元,记销完产品的总利润为
地的产品至少120吨,且每吨售价不得低于1440元,记销完产品的总利润为![]() 元,求
元,求![]() 关于
关于![]() 的函数表达式,及最大总利润.
的函数表达式,及最大总利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
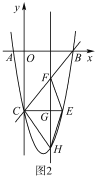
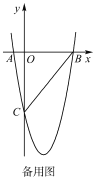
【题目】如图![]() ,在平面直角角坐标系中,已知抛物线
,在平面直角角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点.
两点.
(1)求抛物线的函数表达式;
(2)如图![]() ,
,![]() 轴与抛物线相交于点
轴与抛物线相交于点![]() ,点
,点![]() 是直线
是直线![]() 下方抛物线上的动点,过点
下方抛物线上的动点,过点![]() 且与
且与![]() 轴平行的直线与
轴平行的直线与![]() ,
,![]() 分别交于点
分别交于点![]() 试探究当点
试探究当点![]() 运动到何处时,线段
运动到何处时,线段![]() 的最长,求点
的最长,求点![]() 的坐标;
的坐标;
(3)若点![]() 为抛物线的顶点,点
为抛物线的顶点,点![]() 是该抛物线上的一点,在
是该抛物线上的一点,在![]() 轴、
轴、![]() 轴上分别找点
轴上分别找点![]() ,使四边形
,使四边形![]() 的周长最小,请求出点
的周长最小,请求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
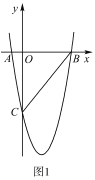
【题目】如图1,经过原点O的抛物线y=ax2+bx(a≠0)与x轴交于另一点A(3,0),在第一象限内与直线y=x交于点B(4,t).
(1)求这条抛物线的表达式;
(2)在直线OB下方的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积最大,求点C的坐标;
(3)如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() ,(
,(![]() 左
左![]() 右),交y轴于点C,△AOC的周长为12,sin∠CBA=
右),交y轴于点C,△AOC的周长为12,sin∠CBA=![]() ,则下列结论:①A点坐标(-3,0);②a=
,则下列结论:①A点坐标(-3,0);②a=![]() ;③点B坐标(8,0);④对称轴x=
;③点B坐标(8,0);④对称轴x=![]() .其中正确的有( )个.
.其中正确的有( )个.
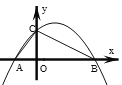
A. 4B. 3C. 2D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com