
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 为
为![]() 上一点,
上一点,![]() 为
为![]() 的切线,
的切线,![]() 于点
于点![]() ,分别交
,分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点.
两点.

(1)求证:![]() ;
;
(2)若![]() 的半径为
的半径为![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)MC=![]() .
.
【解析】
(1)连接OC,利用切线的性质可知∠OCA+∠ACM=90°,结合已知OM⊥AB可得∠ACM=∠ODA=∠CDM,即可证明;
(2)易证△AOD∽△ACB,从而根据相似三角形的性质可得![]() ,由勾股定理可求BC=
,由勾股定理可求BC=![]() ,进而求OD=
,进而求OD=![]() ,在Rt△OCM中利用列方程勾股定理即可求出MC.
,在Rt△OCM中利用列方程勾股定理即可求出MC.
解:(1)连接OC,
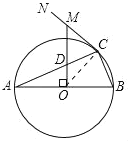
∵CN为⊙O的切线,
∴OC⊥CM,∠OCA+∠ACM=90°,
∵OM⊥AB,
∴∠OAC+∠ODA=90°,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠ACM=∠ODA=∠CDM,
∴MD=MC;
(2)由题意可知AB=5×2=10,AC=4![]() ,
,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴BC=![]() =
=![]() ,
,
∵∠AOD=∠ACB,∠A=∠A,
∴△AOD∽△ACB,
∴![]() 即
即![]() ,
,
可得:OD=![]() ,
,
设MC=MD=x,在Rt△OCM中,由勾股定理得:(x+![]() )2=x2+52,
)2=x2+52,
解得:x=![]() ,
,
即MC=![]() .
.


科目:初中数学 来源: 题型:
【题目】在某校开展的“好书伴我成长”课外阅读活动中,为了解八年级学生的课外阅读情况,随机抽查部分学生,并对其课外阅读量进行统计分析,绘制成图1、图2两幅尚不完整的统计图,请根据图中信息,解答下列问题:
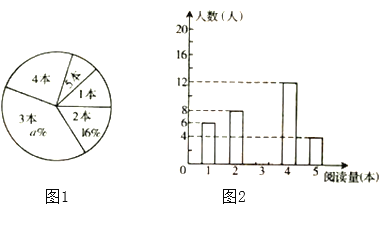
(1)求被抽查的学生人数及课外阅读量的平均数;
(2)求扇形统计图中![]() 的值;
的值;
(3)根据样本数据,估计该校八年级800名学生在本次活动中课外阅读量多于2本的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由7个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
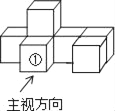
A. 主视图改变,俯视图改变 B. 左视图改变,俯视图改变
C. 俯视图不变,左视图改变 D. 主视图不变,左视图不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级数学小组在课外活动中,研究了同一坐标系中两个反比例函数![]() 与
与![]()
![]() 在第一象限图象的性质,经历了如下探究过程:
在第一象限图象的性质,经历了如下探究过程:
操作猜想:
(1)如图①,当![]() ,
,![]() 时,在
时,在![]() 轴的正方向上取一点
轴的正方向上取一点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .当
.当![]() 时,
时,![]() ________,
________,![]() ________,
________,![]() ________;当
________;当![]() 时,
时,![]() ________,
________,![]() ________,
________,![]() ________;当
________;当![]() 时,猜想
时,猜想![]() ________.
________.

数学思考:
(2)在![]() 轴的正方向上任意取点
轴的正方向上任意取点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 于点
于点![]() 、交
、交![]() 于点
于点![]() ,请用含
,请用含![]() 、
、![]() 的式子表示
的式子表示![]() 的值,并利用图②加以证明.
的值,并利用图②加以证明.

推广应用:
(3)如图③,若![]() ,
,![]() ,在
,在![]() 轴的正方向上分别取点
轴的正方向上分别取点![]() 、
、![]()
![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 于点
于点![]() 、
、![]() ,交
,交![]() 于点
于点![]() 、
、![]() ,是否存在四边形
,是否存在四边形![]() 是正方形?如果存在,求
是正方形?如果存在,求![]() 的长和点
的长和点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国科学技术馆有“圆与非圆”展品,涉及了“等宽曲线”的知识.因为圆的任何一对平行切线的距离总是相等的,所以圆是“等宽曲线”.除了例以外,还有一些几何图形也是“等宽曲线”,如勒洛只角形(图1),它是分别以等边三角形的征个顶点为圆心,以边长为半径,在另两个顶点间画一段圆弧.三段圆弧围成的曲边三角形.图2是等宽的勒洛三角形和圆.
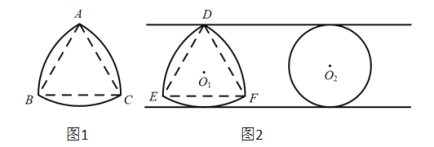
下列说法中错误的是( )
A.勒洛三角形是轴对称图形
B.图1中,点A到![]() 上任意一点的距离都相等
上任意一点的距离都相等
C.图2中,勒洛三角形上任意一点到等边三角形DEF的中心![]() 的距离都相等
的距离都相等
D.图2中,勒洛三角形的周长与圆的周长相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店连续一至四月销售额的增长率都相同,今年2月份的销售额是2万元,4月份的销售额是2.88万元.该商店销售额每月的增长率是多少?1月份的销售额是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com