
【题目】某校九年级数学小组在课外活动中,研究了同一坐标系中两个反比例函数![]() 与
与![]()
![]() 在第一象限图象的性质,经历了如下探究过程:
在第一象限图象的性质,经历了如下探究过程:
操作猜想:
(1)如图①,当![]() ,
,![]() 时,在
时,在![]() 轴的正方向上取一点
轴的正方向上取一点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .当
.当![]() 时,
时,![]() ________,
________,![]() ________,
________,![]() ________;当
________;当![]() 时,
时,![]() ________,
________,![]() ________,
________,![]() ________;当
________;当![]() 时,猜想
时,猜想![]() ________.
________.

数学思考:
(2)在![]() 轴的正方向上任意取点
轴的正方向上任意取点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 于点
于点![]() 、交
、交![]() 于点
于点![]() ,请用含
,请用含![]() 、
、![]() 的式子表示
的式子表示![]() 的值,并利用图②加以证明.
的值,并利用图②加以证明.

推广应用:
(3)如图③,若![]() ,
,![]() ,在
,在![]() 轴的正方向上分别取点
轴的正方向上分别取点![]() 、
、![]()
![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 于点
于点![]() 、
、![]() ,交
,交![]() 于点
于点![]() 、
、![]() ,是否存在四边形
,是否存在四边形![]() 是正方形?如果存在,求
是正方形?如果存在,求![]() 的长和点
的长和点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.

【答案】(1)当![]() 时,
时,![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() (2)
(2)![]() ,理由见解析;(3)存在,
,理由见解析;(3)存在,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,理由见解析
,理由见解析
【解析】
(1)只需根据ABOA=2及ACOA=6就可解决问题;
(2)由AB·OA=k1,AC·OA=k2可得BC·OA= k2-k1,就可得到![]() ;
;
(3)设点B的坐标为(a,b)(a>0,b>0),则有DF=DA=AB=a,OA=b,从而可得到点F的坐标(a,a+b),由k2=12及![]() ,可求得k1=8,根据点B、F分别在两支图像上,可得到ab=8,a(a+b)=12,从而求出a,b的值
,可求得k1=8,根据点B、F分别在两支图像上,可得到ab=8,a(a+b)=12,从而求出a,b的值
(1)当OA=1时,由ABOA=2得AB=2,由ACOA=6得AC=6,则有BC=ACAB=4,所以![]() =2;
=2;
当OA=3时,由ABOA=2得AB=![]() ,由ACOA=6得AC=2,则有BC=ACAB=
,由ACOA=6得AC=2,则有BC=ACAB=![]() ,所以
,所以![]() =2;
=2;
当![]() 时,猜想
时,猜想![]() .
.

(2)![]()
证明:∵![]() ,
,![]() ,
,
∴![]() ,
,
∴ ![]() .
.

(3)若四边形![]() 是正方形,
是正方形,
设点![]() 的坐标为
的坐标为![]() (
(![]() ,
,![]() ),
),
则有![]() ,
,![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
解得:![]() .
.
∵点![]() 在
在![]() 图象上,点
图象上,点![]() 在
在![]() 图象上,
图象上,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=![]() x2+
x2+![]() x-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线l经过A,C两点,连接BC.
x-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线l经过A,C两点,连接BC.
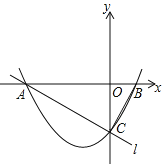
(1)求直线l的解析式;
(2)若直线x=m(m<0)与该抛物线在第三象限内交于点E,与直线l交于点D,连接OD.当OD⊥AC时,求线段DE的长;
(3)取点G(0,-1),连接AG,在第一象限内的抛物线上,是否存在点P,使∠BAP=∠BCO-∠BAG?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数![]() 的图像与边长是6的正方形
的图像与边长是6的正方形![]() 的两边
的两边![]() ,
,![]() 分别相交于
分别相交于![]() ,
,![]() 两点.
两点.
(1)若点![]() 是
是![]() 边的中点,求反比例函数
边的中点,求反比例函数![]() 的解析式和点
的解析式和点![]() 的坐标;
的坐标;
(2)若![]() ,求直线
,求直线![]() 的解析式及
的解析式及![]() 的面积
的面积

查看答案和解析>>
科目:初中数学 来源: 题型:
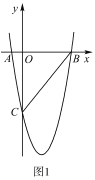
【题目】如图![]() ,在平面直角角坐标系中,已知抛物线
,在平面直角角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点.
两点.
(1)求抛物线的函数表达式;
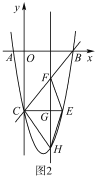
(2)如图![]() ,
,![]() 轴与抛物线相交于点
轴与抛物线相交于点![]() ,点
,点![]() 是直线
是直线![]() 下方抛物线上的动点,过点
下方抛物线上的动点,过点![]() 且与
且与![]() 轴平行的直线与
轴平行的直线与![]() ,
,![]() 分别交于点
分别交于点![]() 试探究当点
试探究当点![]() 运动到何处时,线段
运动到何处时,线段![]() 的最长,求点
的最长,求点![]() 的坐标;
的坐标;
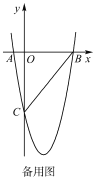
(3)若点![]() 为抛物线的顶点,点
为抛物线的顶点,点![]() 是该抛物线上的一点,在
是该抛物线上的一点,在![]() 轴、
轴、![]() 轴上分别找点
轴上分别找点![]() ,使四边形
,使四边形![]() 的周长最小,请求出点
的周长最小,请求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() =
=![]() ﹣3与
﹣3与![]() =
=![]() +1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结沦:①无论x取何值,
+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结沦:①无论x取何值,![]() 的值总是正数;②2a=1;③当x=0时,
的值总是正数;②2a=1;③当x=0时,![]() ﹣
﹣![]() =4;④2AB=3AC.其中正确结论是______.(填序号)
=4;④2AB=3AC.其中正确结论是______.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,经过原点O的抛物线y=ax2+bx(a≠0)与x轴交于另一点A(3,0),在第一象限内与直线y=x交于点B(4,t).
(1)求这条抛物线的表达式;
(2)在直线OB下方的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积最大,求点C的坐标;
(3)如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx+2与x轴、y轴分别交于点A(-1,0)和点B,与反比例函数y=![]() 的图象在第一象限内交于点C(1,n).
的图象在第一象限内交于点C(1,n).
(1)求k的值;
(2)求反比例函数的解析式;
(3)过x轴上的点D(a,0)作平行于y轴的直线l(a>1),分别与直线AB和双曲线y=![]() 交于点P、Q,且PQ=2QD,求点D的坐标.
交于点P、Q,且PQ=2QD,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机店销售![]() 部
部![]() 型和
型和![]() 部
部![]() 型手机的利润为
型手机的利润为![]() 元,销售
元,销售![]() 部
部![]() 型和
型和![]() 部
部![]() 型手机的利润为
型手机的利润为![]() 元.
元.
(1)求每部![]() 型手机和
型手机和![]() 型手机的销售利润;
型手机的销售利润;
(2)该手机店计划一次购进![]() ,
,![]() 两种型号的手机共
两种型号的手机共![]() 部,其中
部,其中![]() 型手机的进货量不超过
型手机的进货量不超过![]() 型手机的
型手机的![]() 倍,设购进
倍,设购进![]() 型手机
型手机![]() 部,这
部,这![]() 部手机的销售总利润为
部手机的销售总利润为![]() 元.
元.
①求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②该手机店购进![]() 型、
型、![]() 型手机各多少部,才能使销售总利润最大?
型手机各多少部,才能使销售总利润最大?
(3)在(2)的条件下,该手机店实际进货时,厂家对![]() 型手机出厂价下调
型手机出厂价下调![]() 元,且限定手机店最多购进
元,且限定手机店最多购进![]() 型手机
型手机![]() 部,若手机店保持同种手机的售价不变,设计出使这
部,若手机店保持同种手机的售价不变,设计出使这![]() 部手机销售总利润最大的进货方案.
部手机销售总利润最大的进货方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com