
【题目】如图,在平面直角坐标系中,已知抛物线y=![]() x2+
x2+![]() x-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线l经过A,C两点,连接BC.
x-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线l经过A,C两点,连接BC.
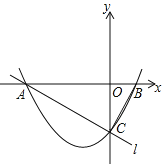
(1)求直线l的解析式;
(2)若直线x=m(m<0)与该抛物线在第三象限内交于点E,与直线l交于点D,连接OD.当OD⊥AC时,求线段DE的长;
(3)取点G(0,-1),连接AG,在第一象限内的抛物线上,是否存在点P,使∠BAP=∠BCO-∠BAG?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x2;(2)
x2;(2)![]() ;(3)P(
;(3)P(![]() ,
,![]() )
)
【解析】
(1)根据题目中的函数解析式可以求得点A和点C的坐标,从而可以求得直线l的函数解析式;
(2)根据题意作出合适的辅助线,利用三角形相似和勾股定理可以解答本题;
(3)根据题意画出相应的图形,然后根据锐角三角函数可以求得∠OAC=∠OCB,然后根据题目中的条件和图形,利用锐角三角函数和勾股定理即可解答本题.
(1)∵抛物线y=![]() x2+
x2+![]() x-2,
x-2,
∴当y=0时,得x1=1,x2=-4,当x=0时,y=-2,
∵抛物线y=![]() x2+
x2+![]() x-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,
x-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,
∴点A的坐标为(-4,0),点B(1,0),点C(0,-2),
∵直线l经过A,C两点,设直线l的函数解析式为y=kx+b,
![]() ,得
,得 ,
,
即直线l的函数解析式为y=![]() x2;
x2;
(2)直线ED与x轴交于点F,如图1所示,
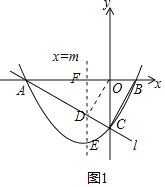
由(1)可得,
AO=4,OC=2,∠AOC=90°,
∴AC=2![]() ,
,
∴OD=![]() ,
,
∵OD⊥AC,OA⊥OC,∠OAD=∠CAO,
∴△AOD∽△ACO,
∴![]() ,
,
即![]() ,得AD=
,得AD=![]() ,
,
∵EF⊥x轴,∠ADC=90°,
∴EF∥OC,
∴△ADF∽△ACO,
∴![]() ,
,
解得,AF=![]() ,DF=
,DF=![]() ,
,
∴OF=4-![]() =
=![]() ,
,
∴m=-![]() ,
,
当m=-![]() 时,y=
时,y=![]() ×(
×(![]() )2+
)2+![]() ×(-
×(-![]() )-2=-
)-2=-![]() ,
,
∴EF=![]() ,
,
∴DE=EF-FD=![]()
![]() =
=![]() ;
;
(3)存在点P,使∠BAP=∠BCO-∠BAG,
理由:作GM⊥AC于点M,作PN⊥x轴于点N,如图2所示,

∵点A(-4,0),点B(1,0),点C(0,-2),
∴OA=4,OB=1,OC=2,
∴tan∠OAC=![]() ,tan∠OCB=
,tan∠OCB=![]() ,AC=2
,AC=2![]() ,
,
∴∠OAC=∠OCB,
∵∠BAP=∠BCO-∠BAG,∠GAM=∠OAC-∠BAG,
∴∠BAP=∠GAM,
∵点G(0,-1),AC=2![]() ,OA=4,
,OA=4,
∴OG=1,GC=1,
∴AG=![]() ,
,
![]() ,即
,即![]() ,
,
解得,GM=![]() ,
,
∴AM=![]() ,
,
∴tan∠GAM=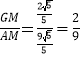 ,
,
∴tan∠PAN=![]() ,
,
设点P的坐标为(n,![]() n2+
n2+![]() n-2),
n-2),
∴AN=4+n,PN=![]() n2+
n2+![]() n-2,
n-2,
∴![]() ,
,
解得,n1=![]() ,n2=-4(舍去),
,n2=-4(舍去),
当n=![]() 时,
时,![]() n2+
n2+![]() n-2=
n-2=![]() ,
,
∴点P的坐标为(![]() ,
,![]() ),
),
即存在点P(![]() ,
,![]() ),使∠BAP=∠BCO-∠BAG.
),使∠BAP=∠BCO-∠BAG.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 用适当的统计图表示某班同学戴眼镜和不戴眼镜所占的比例,应绘制折线统计图
B. 为了解我市某区中小学生每月零花钱的情况,随机抽取其中800名学生进行调查,这次调查的样本是800名学生
C. “任意画出一个平行四边形,它是中心对称图形”是必然事件
D. 若点![]() 在第二象限,则点
在第二象限,则点![]() 在第一象限
在第一象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方![]() 米处的点C出发,沿坡角为30°的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB∥DE.求旗杆AB的高度.(参考数据:sin37°≈
米处的点C出发,沿坡角为30°的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB∥DE.求旗杆AB的高度.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ,计算结果保留根号)
,计算结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某校开展的“好书伴我成长”课外阅读活动中,为了解八年级学生的课外阅读情况,随机抽查部分学生,并对其课外阅读量进行统计分析,绘制成图1、图2两幅尚不完整的统计图,请根据图中信息,解答下列问题:
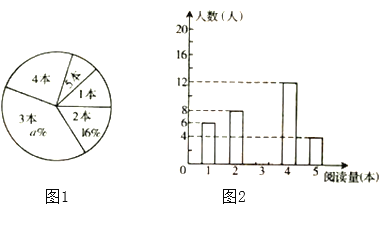
(1)求被抽查的学生人数及课外阅读量的平均数;
(2)求扇形统计图中![]() 的值;
的值;
(3)根据样本数据,估计该校八年级800名学生在本次活动中课外阅读量多于2本的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将![]() 沿弦
沿弦![]() 折叠,使折叠后的劣弧
折叠,使折叠后的劣弧![]() 恰好经过圆心O,连接
恰好经过圆心O,连接![]() 并延长交
并延长交![]() 于点C,点P是优弧
于点C,点P是优弧![]() 上的动点,连接
上的动点,连接![]() .
.
(1)如图,用尺规面出折叠后的劣弧![]() 所在圆的圆心
所在圆的圆心![]() ,并求出
,并求出![]() 的度数;
的度数;
(2)如图,若![]() 是
是![]() 的切线,
的切线,![]() ,求线段
,求线段![]() 的长;
的长;
(3)如图,连接![]() ,过点B作
,过点B作![]() 的重线,交
的重线,交![]() 的延长线于点D,求证:
的延长线于点D,求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 在射线
在射线![]() 上,以
上,以![]() 为半径的
为半径的![]() 交边
交边![]() 于点
于点![]() (点
(点![]() 与点
与点![]() 不重合),联结
不重合),联结![]() 、
、![]() ,设
,设![]() ,
,![]() .
.
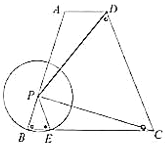
(1)求证:![]() ;
;
(2)求![]() 关于
关于![]() 的函数解析式,并写出定义域;
的函数解析式,并写出定义域;
(3)联结![]() ,当
,当![]() 时,以
时,以![]() 为圆心半径为
为圆心半径为![]() 的
的![]() 与
与![]() 相交,求
相交,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,双曲线![]() 经过矩形OABC的边BC的中点E,交AB于点D.设点B的坐标为(m,n).
经过矩形OABC的边BC的中点E,交AB于点D.设点B的坐标为(m,n).
(1)直接写出点E的坐标,并求出点D的坐标;(用含m,n的代数式表示)
(2)若梯形ODBC的面积为![]() ,求双曲线的函数解析式.
,求双曲线的函数解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级数学小组在课外活动中,研究了同一坐标系中两个反比例函数![]() 与
与![]()
![]() 在第一象限图象的性质,经历了如下探究过程:
在第一象限图象的性质,经历了如下探究过程:
操作猜想:
(1)如图①,当![]() ,
,![]() 时,在
时,在![]() 轴的正方向上取一点
轴的正方向上取一点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .当
.当![]() 时,
时,![]() ________,
________,![]() ________,
________,![]() ________;当
________;当![]() 时,
时,![]() ________,
________,![]() ________,
________,![]() ________;当
________;当![]() 时,猜想
时,猜想![]() ________.
________.

数学思考:
(2)在![]() 轴的正方向上任意取点
轴的正方向上任意取点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 于点
于点![]() 、交
、交![]() 于点
于点![]() ,请用含
,请用含![]() 、
、![]() 的式子表示
的式子表示![]() 的值,并利用图②加以证明.
的值,并利用图②加以证明.

推广应用:
(3)如图③,若![]() ,
,![]() ,在
,在![]() 轴的正方向上分别取点
轴的正方向上分别取点![]() 、
、![]()
![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 于点
于点![]() 、
、![]() ,交
,交![]() 于点
于点![]() 、
、![]() ,是否存在四边形
,是否存在四边形![]() 是正方形?如果存在,求
是正方形?如果存在,求![]() 的长和点
的长和点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com