
【题目】如图,抛物线![]() =
=![]() ﹣3与
﹣3与![]() =
=![]() +1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结沦:①无论x取何值,
+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结沦:①无论x取何值,![]() 的值总是正数;②2a=1;③当x=0时,
的值总是正数;②2a=1;③当x=0时,![]() ﹣
﹣![]() =4;④2AB=3AC.其中正确结论是______.(填序号)
=4;④2AB=3AC.其中正确结论是______.(填序号)

【答案】①④
【解析】
利用二次函数的性质得到y2的最小值为1,则可对①进行判断;把A点坐标代入y1=a(x+2)2-3中求出a,则可对②进行判断;分别计算x=0时两函数的对应值,再计算y2-y1的值,则可对③进行判断;利用抛物线的对称性计算出AB和AC,则可对④进行判断.
解:∵y2=![]() +1,
+1,
∴y2的最小值为1,所以①正确;
把A(1,3)代入y1=a(x+2)2-3得a(1+2)2-3=3,
∴3a=2,所以②错误;
当x=0时,y1=![]() (x+2)2-3=-
(x+2)2-3=-![]() , y2=
, y2=![]() +1=
+1=![]() ,
,
∴y2-y1=![]() +
+![]() =
=![]() ,所以③错误;
,所以③错误;
抛物线y1=a (x+2)2-3的对称轴为直线x=-2,抛物线y2=![]() +1
+1
的对称轴为直线x=3,
∴AB=2×3=6,AC=2×2=4,
∴2AB=3AC,所以④正确.
故答案为①④.


科目:初中数学 来源: 题型:
【题目】如图,将![]() 沿弦
沿弦![]() 折叠,使折叠后的劣弧
折叠,使折叠后的劣弧![]() 恰好经过圆心O,连接
恰好经过圆心O,连接![]() 并延长交
并延长交![]() 于点C,点P是优弧
于点C,点P是优弧![]() 上的动点,连接
上的动点,连接![]() .
.
(1)如图,用尺规面出折叠后的劣弧![]() 所在圆的圆心
所在圆的圆心![]() ,并求出
,并求出![]() 的度数;
的度数;
(2)如图,若![]() 是
是![]() 的切线,
的切线,![]() ,求线段
,求线段![]() 的长;
的长;
(3)如图,连接![]() ,过点B作
,过点B作![]() 的重线,交
的重线,交![]() 的延长线于点D,求证:
的延长线于点D,求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
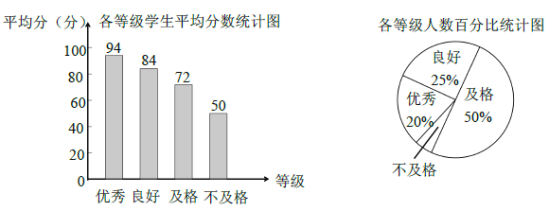
【题目】《中学生体质健康标准》规定学生体质健康等级标准为:90分及以上为优秀;80分~89分为良好;60分~79分为及格;59分及以下为不及格. 某校从九年级学生中随机抽取了![]() 的学生进行了体质测试,得分情况如下图.
的学生进行了体质测试,得分情况如下图.
(1)在抽取的学生中不及格人数所占的百分比是 ,它的圆心角度数为 度.
(2)小明按以下方法计算出抽取的学生平均得分是:![]() . 根据所学的统计知识判断小明的计算是否正确,若不正确,请计算正确结果.
. 根据所学的统计知识判断小明的计算是否正确,若不正确,请计算正确结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
(k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
(1)求反比例函数的解析式及B点的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级数学小组在课外活动中,研究了同一坐标系中两个反比例函数![]() 与
与![]()
![]() 在第一象限图象的性质,经历了如下探究过程:
在第一象限图象的性质,经历了如下探究过程:
操作猜想:
(1)如图①,当![]() ,
,![]() 时,在
时,在![]() 轴的正方向上取一点
轴的正方向上取一点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .当
.当![]() 时,
时,![]() ________,
________,![]() ________,
________,![]() ________;当
________;当![]() 时,
时,![]() ________,
________,![]() ________,
________,![]() ________;当
________;当![]() 时,猜想
时,猜想![]() ________.
________.

数学思考:
(2)在![]() 轴的正方向上任意取点
轴的正方向上任意取点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 于点
于点![]() 、交
、交![]() 于点
于点![]() ,请用含
,请用含![]() 、
、![]() 的式子表示
的式子表示![]() 的值,并利用图②加以证明.
的值,并利用图②加以证明.

推广应用:
(3)如图③,若![]() ,
,![]() ,在
,在![]() 轴的正方向上分别取点
轴的正方向上分别取点![]() 、
、![]()
![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 于点
于点![]() 、
、![]() ,交
,交![]() 于点
于点![]() 、
、![]() ,是否存在四边形
,是否存在四边形![]() 是正方形?如果存在,求
是正方形?如果存在,求![]() 的长和点
的长和点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景
(1)如图1,△ABC中,DE∥BC分别交AB,AC于D,E两点,过点E作EF∥AB交BC于点F.请按图示数据填空:
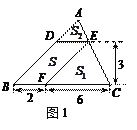
四边形DBFE的面积![]() ,
,
△EFC的面积![]() ,
,
△ADE的面积![]() .
.
探究发现
(2)在(1)中,若![]() ,
,![]() ,DE与BC间的距离为
,DE与BC间的距离为![]() .请证明
.请证明![]() .
.
拓展迁移
(3)如图2,□DEFG的四个顶点在△ABC的三边上,若△ADG、△DBE、△GFC的面积分别为2、5、3,试利用(2)中的结论求△ABC的面积.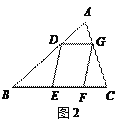
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“特色江苏,美好生活”,第十届江苏省园艺博览会在扬州举行.圆圆和满满同学分析网上关于园博会的信息,发现最具特色的场馆有:扬州园,苏州园,盐城园,无锡园.他们准备周日下午去参观游览,各自在这四个园中任选一个,每个园被选中的可能性相同.
(1)圆圆同学在四个备选园中选中扬州园的概率是 .
(2)用树状图或列表法求出圆圆和满满他们选中同一个园参观的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
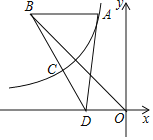
【题目】如图,点A是双曲线y=![]() 上一点,过A作AB∥x轴,交直线y=-x于点B,点D是x轴上一点,连接BD交双曲线于点C,连接AD,若BC:CD=3:2,△ABD的面积为
上一点,过A作AB∥x轴,交直线y=-x于点B,点D是x轴上一点,连接BD交双曲线于点C,连接AD,若BC:CD=3:2,△ABD的面积为![]() ,tan∠ABD=
,tan∠ABD=![]() ,则k的值为( )
,则k的值为( )
A. -![]() B. -3C. -2D.
B. -3C. -2D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com