
【题目】问题背景
(1)如图1,△ABC中,DE∥BC分别交AB,AC于D,E两点,过点E作EF∥AB交BC于点F.请按图示数据填空:
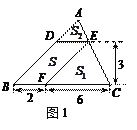
四边形DBFE的面积![]() ,
,
△EFC的面积![]() ,
,
△ADE的面积![]() .
.
探究发现
(2)在(1)中,若![]() ,
,![]() ,DE与BC间的距离为
,DE与BC间的距离为![]() .请证明
.请证明![]() .
.
拓展迁移
(3)如图2,□DEFG的四个顶点在△ABC的三边上,若△ADG、△DBE、△GFC的面积分别为2、5、3,试利用(2)中的结论求△ABC的面积.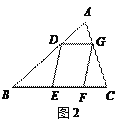
科目:初中数学 来源: 题型:
【题目】为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:
捐款的数额(单位:元) | 5 | 10 | 20 | 50 | 100 |
人数(单位:个) | 2 | 4 | 5 | 3 | 1 |
关于这15名同学所捐款的数额,下列说法正确的是
A.众数是100 B.平均数是30 C.极差是20 D.中位数是20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,DE分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连CF
(1)求证:四边形BCFE是菱形;
(2)若CE=6,∠BEF=120°,求菱形BCFE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() =
=![]() ﹣3与
﹣3与![]() =
=![]() +1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结沦:①无论x取何值,
+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结沦:①无论x取何值,![]() 的值总是正数;②2a=1;③当x=0时,
的值总是正数;②2a=1;③当x=0时,![]() ﹣
﹣![]() =4;④2AB=3AC.其中正确结论是______.(填序号)
=4;④2AB=3AC.其中正确结论是______.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
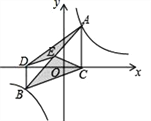
【题目】如图,点A,B在反比例函数![]() (k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是______.
(k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作体验)
如图①,已知线段AB和直线l,用直尺和圆规在l上作出所有的点P,使得∠APB=30°.

如图②,小明的作图方法如下:
第一步:分别以点A、B为圆心,AB长为半径作弧,两弧在AB上方交于点O;
第二步:连接OA、OB;
第三步:以O为圆心,OA长为半径作⊙O,交l于P1,P2.
所以图中P1,P2即为所求的点.
(1) 在图②中,连接P1A,P1 B,说明∠A P1B=30°;
(方法迁移)
(2)如图③,用直尺和圆规在矩形ABCD内作出所有的点P,使得∠BPC=45°.
(不写作法,保留作图痕迹)

(深入探究)
(3)已知矩形ABCD,BC=2,AB=m,P为AD边上的点,若满足∠BPC=45°的点P恰有两个,则m的取值范围为 .
(4)已知矩形ABCD,AB=3,BC=2,P为矩形ABCD内一点,且∠BPC=135°,若点P绕点A逆时针旋转90°到点Q,则PQ的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,点B为⊙O上一点,PA切⊙O于点A,PB与AC的延长线交于点M,∠CAB=![]() ∠APB.
∠APB.
(1)求证:PB是⊙O的切线;
(2)当sinM=![]() ,OA=2时,求MB,AB的长.
,OA=2时,求MB,AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片![]() 中,
中,![]() ,
,![]() ,把
,把![]() 沿对角线
沿对角线![]() 折叠,点
折叠,点![]() 落在
落在![]() 处,
处,![]() 交
交![]() 于点
于点![]() 。再次折叠,使点
。再次折叠,使点![]() 与点
与点![]() 重合,
重合,![]() 为折痕,点
为折痕,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() 交
交![]() 于点
于点![]() .
.
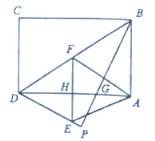
(1)求![]() 的值;
的值;
(2)求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com