
【题目】如图,在矩形纸片![]() 中,
中,![]() ,
,![]() ,把
,把![]() 沿对角线
沿对角线![]() 折叠,点
折叠,点![]() 落在
落在![]() 处,
处,![]() 交
交![]() 于点
于点![]() 。再次折叠,使点
。再次折叠,使点![]() 与点
与点![]() 重合,
重合,![]() 为折痕,点
为折痕,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() 交
交![]() 于点
于点![]() .
.
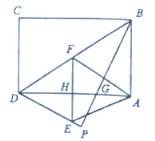
(1)求![]() 的值;
的值;
(2)求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() 的长为
的长为![]() .
.
【解析】
(1)根据翻折变换的性质可知∠C=∠BAG=90°,PD=AB=CD,∠AGB=∠DGP,故可得出![]() .,可知GD=GB,故AG+GB=AD,设AG=x,则GB=8-x,在Rt△ABG中利用勾股定理即可求出AG的长,进而得出tan∠ABG的值;
.,可知GD=GB,故AG+GB=AD,设AG=x,则GB=8-x,在Rt△ABG中利用勾股定理即可求出AG的长,进而得出tan∠ABG的值;
(3)由△AEF是△DEF翻折而成可知EF垂直平分AD,故HD=![]() AD=4,再根据tan∠ABG即可得出EH的长,同理可得HF是△ABD的中位线,故可得出HF的长,由EF=EH+HF即可得出结论.
AD=4,再根据tan∠ABG即可得出EH的长,同理可得HF是△ABD的中位线,故可得出HF的长,由EF=EH+HF即可得出结论.
(1)证明:∵△BDP由△BDC翻折而成,
∴∠P=∠BAG=90°,PD=AB=CD,∠AGB=∠DGP,
∴∠ABG=∠ADE,
在△ABG与△C′DG中,
∵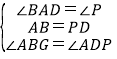 ,
,
∴△ABG≌△C′DG(AAS);.
![]() .
.
设![]() ,则
,则![]() .
.
在![]() 中,可得
中,可得![]() .
.
解得,![]() .
.
![]() .
.
(2)易得![]() 垂直平分
垂直平分![]() ,所以
,所以![]() .
.
由![]() ,可得
,可得![]() .
.
![]() ,解得
,解得![]() .
.
易得![]() 是
是![]() 的中位线,所以
的中位线,所以![]() .
.
![]() 的长为
的长为![]() .
.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】问题背景
(1)如图1,△ABC中,DE∥BC分别交AB,AC于D,E两点,过点E作EF∥AB交BC于点F.请按图示数据填空:
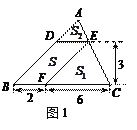
四边形DBFE的面积![]() ,
,
△EFC的面积![]() ,
,
△ADE的面积![]() .
.
探究发现
(2)在(1)中,若![]() ,
,![]() ,DE与BC间的距离为
,DE与BC间的距离为![]() .请证明
.请证明![]() .
.
拓展迁移
(3)如图2,□DEFG的四个顶点在△ABC的三边上,若△ADG、△DBE、△GFC的面积分别为2、5、3,试利用(2)中的结论求△ABC的面积.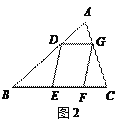
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李宁准备完成题目;解二元一次方程组![]() ,发现系数“□”印刷不清楚.
,发现系数“□”印刷不清楚.
(1)他把“□”猜成3,请你解二元一次方程组![]() ;
;
(2)张老师说:“你猜错了”,我看到该题标准答案的结果x、y是一对相反数,通过计算说明原题中“□”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程x2+4x﹣9=0时,原方程可变形为( )
A. (x+2)2=1 B. (x+2)2=7 C. (x+2)2=13 D. (x+2)2=19
查看答案和解析>>
科目:初中数学 来源: 题型:
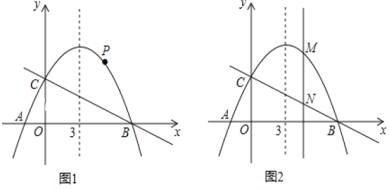
【题目】如图, 已知抛物线![]() 的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧)与y轴交于C点 .
的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧)与y轴交于C点 .
(1)求抛物线的解析式和A、B两点的坐标;
(2)若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),则是否存在一点P,使△PBC的面积最大.若存在,请求出△PBC的最大面积;若不存在,试说明理由;
(3)若M是抛物线上任意一点,过点M作y轴的平行线,交直线BC于点N,当MN=3时,求M点的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花店用3600元按批发价购买了一批花卉.若将批发价降低10%,则可以多购买该花卉20盆.市场调查反映,该花卉每盆售价25元时,每天可卖出25盆.若调整价格,每盆花卉每涨价1元,每天要少卖出1盆.
(1)该花卉每盆批发价是多少元?
(2)若每天所得的销售利润为200元时,且销量尽可能大,该花卉每盆售价是多少元?
(3)为了让利给顾客,该花店决定每盆花卉涨价不超过5元,问该花卉一天最大的销售利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com