
【题目】如图,AB、BC为![]() 的两条弦,
的两条弦,![]() ,则
,则![]() 的度数为( ).
的度数为( ).
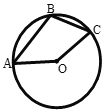
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
【题目】为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:
捐款的数额(单位:元) | 5 | 10 | 20 | 50 | 100 |
人数(单位:个) | 2 | 4 | 5 | 3 | 1 |
关于这15名同学所捐款的数额,下列说法正确的是
A.众数是100 B.平均数是30 C.极差是20 D.中位数是20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作体验)
如图①,已知线段AB和直线l,用直尺和圆规在l上作出所有的点P,使得∠APB=30°.

如图②,小明的作图方法如下:
第一步:分别以点A、B为圆心,AB长为半径作弧,两弧在AB上方交于点O;
第二步:连接OA、OB;
第三步:以O为圆心,OA长为半径作⊙O,交l于P1,P2.
所以图中P1,P2即为所求的点.
(1) 在图②中,连接P1A,P1 B,说明∠A P1B=30°;
(方法迁移)
(2)如图③,用直尺和圆规在矩形ABCD内作出所有的点P,使得∠BPC=45°.
(不写作法,保留作图痕迹)

(深入探究)
(3)已知矩形ABCD,BC=2,AB=m,P为AD边上的点,若满足∠BPC=45°的点P恰有两个,则m的取值范围为 .
(4)已知矩形ABCD,AB=3,BC=2,P为矩形ABCD内一点,且∠BPC=135°,若点P绕点A逆时针旋转90°到点Q,则PQ的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,点B为⊙O上一点,PA切⊙O于点A,PB与AC的延长线交于点M,∠CAB=![]() ∠APB.
∠APB.
(1)求证:PB是⊙O的切线;
(2)当sinM=![]() ,OA=2时,求MB,AB的长.
,OA=2时,求MB,AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗。我市某食品厂为了解市民对去年销量较好的肉馅粽(咸)、豆沙馅粽(甜)、红枣馅粽(甜)、蛋黄馅粽(咸)(以下分别用![]() 表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整)。请根据以上信息回答:
表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整)。请根据以上信息回答:
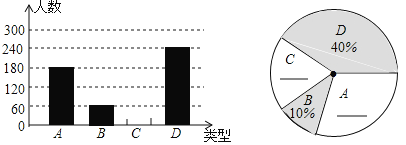
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有7000人,请估计爱吃A粽的人数;
(4)若有外型完全相同的![]() 粽各一个,煮熟后,小王吃了两个。用列表或画树状图的方法,求他吃到的两个粽子都是甜味的概率。
粽各一个,煮熟后,小王吃了两个。用列表或画树状图的方法,求他吃到的两个粽子都是甜味的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形![]() 绕点
绕点![]() 顺时针旋转至正方形
顺时针旋转至正方形![]() ,连接
,连接![]() .
.
(1)如图,求证:![]() ;
;
(2)如图,延长![]() 交
交![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,在不添加任何辅助线的情况下,请直接写出如图中的四个角,使写出的每一个角的大小都等于旋转角.
,在不添加任何辅助线的情况下,请直接写出如图中的四个角,使写出的每一个角的大小都等于旋转角.
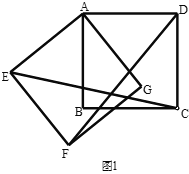
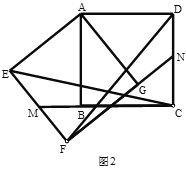
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,易证△ABP∽△PCD,从而得到BPPC=ABCD(不需证明)

探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,结论BPPC=ABCD仍成立吗?请说明理由?
拓展:如图③,在△ABC中,点P是BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=4 ![]() ,CE=3,则DE的长为 .
,CE=3,则DE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片![]() 中,
中,![]() ,
,![]() ,把
,把![]() 沿对角线
沿对角线![]() 折叠,点
折叠,点![]() 落在
落在![]() 处,
处,![]() 交
交![]() 于点
于点![]() 。再次折叠,使点
。再次折叠,使点![]() 与点
与点![]() 重合,
重合,![]() 为折痕,点
为折痕,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() 交
交![]() 于点
于点![]() .
.
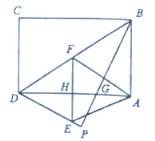
(1)求![]() 的值;
的值;
(2)求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=-![]() (x+4)(x-4)与x轴交于A、B两点,与y轴交于C点,⊙C的半径为2.G为⊙C上一动点,P为AG的中点,则OP的最大值为( )
(x+4)(x-4)与x轴交于A、B两点,与y轴交于C点,⊙C的半径为2.G为⊙C上一动点,P为AG的中点,则OP的最大值为( )
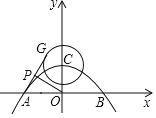
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com