
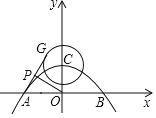
【题目】已知抛物线y=-![]() (x+4)(x-4)与x轴交于A、B两点,与y轴交于C点,⊙C的半径为2.G为⊙C上一动点,P为AG的中点,则OP的最大值为( )
(x+4)(x-4)与x轴交于A、B两点,与y轴交于C点,⊙C的半径为2.G为⊙C上一动点,P为AG的中点,则OP的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程x2+4x﹣9=0时,原方程可变形为( )
A. (x+2)2=1 B. (x+2)2=7 C. (x+2)2=13 D. (x+2)2=19
查看答案和解析>>
科目:初中数学 来源: 题型:
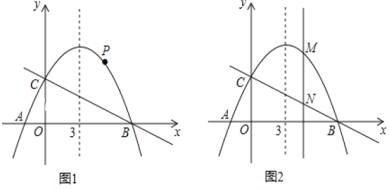
【题目】如图, 已知抛物线![]() 的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧)与y轴交于C点 .
的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧)与y轴交于C点 .
(1)求抛物线的解析式和A、B两点的坐标;
(2)若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),则是否存在一点P,使△PBC的面积最大.若存在,请求出△PBC的最大面积;若不存在,试说明理由;
(3)若M是抛物线上任意一点,过点M作y轴的平行线,交直线BC于点N,当MN=3时,求M点的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若正整数a,b,c(a<b<c)满足a2+b2=c2,则称(a,b,c)为一组“勾股数”.
观察下列两类“勾股数”:
第一类(a是奇数):(3,4,5);(5,12,13);(7,24,25);…
第二类(a是偶数):(6,8,10);(8,15,17);(10,24,26);…
(1)请再写出两组勾股数,每类各写一组;
(2)分别就a为奇数、偶数两种情形,用a表示b和c,并选择其中一种情形证明(a,b,c)是“勾股数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:点Q到图形W上每一个点的距离的最小值称为点Q到图形W的距离.
例如,如图1,正方形ABCD满足A(1,0),B(2,0),C(2,1),D(1,1),那么点O(0,0)到正方形ABCD的距离为1.
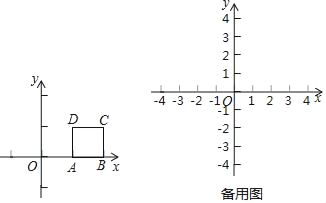
(1)如果⊙P是以(3,4)为圆心,2为半径的圆,那么点O(0,0)到⊙P的距离为 ;
(2)①求点M(3,0)到直线了y=![]() x+4的距离:
x+4的距离:
②如果点N(0,a)到直线y=![]() x+4的距离为2,求a的值;
x+4的距离为2,求a的值;
(3)如果点G(0,b)到抛物线y=x2的距离为3,请直接写出b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
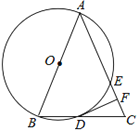
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,请直接写出弧AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花店用3600元按批发价购买了一批花卉.若将批发价降低10%,则可以多购买该花卉20盆.市场调查反映,该花卉每盆售价25元时,每天可卖出25盆.若调整价格,每盆花卉每涨价1元,每天要少卖出1盆.
(1)该花卉每盆批发价是多少元?
(2)若每天所得的销售利润为200元时,且销量尽可能大,该花卉每盆售价是多少元?
(3)为了让利给顾客,该花店决定每盆花卉涨价不超过5元,问该花卉一天最大的销售利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com