
����Ŀ�����壺��Q��ͼ��W��ÿһ����ľ������Сֵ��Ϊ��Q��ͼ��W�ľ��룮
���磬��ͼ1��������ABCD����A��1��0����B��2��0����C��2��1����D��1��1������ô��O��0��0����������ABCD�ľ���Ϊ1��
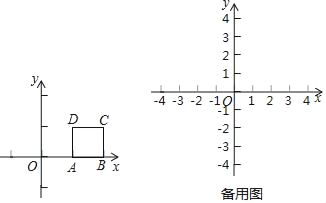
��1�������P���ԣ�3��4��ΪԲ�ģ�2Ϊ�뾶��Բ����ô��O��0��0������P�ľ���Ϊ�� ����
��2�������M��3��0����ֱ����y��![]() x+4�ľ��룺
x+4�ľ��룺
�������N��0��a����ֱ��y��![]() x+4�ľ���Ϊ2����a��ֵ��
x+4�ľ���Ϊ2����a��ֵ��
��3�������G��0��b����������y��x2�ľ���Ϊ3����ֱ��д��b��ֵ��
���𰸡���1��3��2����![]() ��
��![]() ��
��![]() ��3����3��
��3����3��![]()
��������
���ݹ��ɶ����ɵõ�O��0��0���� P�ľ��룻
�ٹ���M��M��M��l������Ϊ��M�䣬��ֱ�������ε����ʿɵ�M��M��MA sin��M��AM��6��![]() ��
��![]() ���Ӷ��õ���M��ֱ��
���Ӷ��õ���M��ֱ��![]() �ľ��룻
�ľ��룻
�ڷ����������N��l���ϱߣ�N��l���±ߣ����������ȵõ�BN�ij�����һ�����ɵõ�a��ֵ��
������������ٵ�G��ԭ�����棻�ڵ�G��ԭ�����棻�������ۼ��ɵõ�b��ֵ��
��1������OP��Բ�ڵ�Q��

������ã�OQΪ��O��0��0������P�ľ��룬
��P��3��4����OP��5����PQ��5��2��3��
�ʴ���3��
��2��������ͼ��ʾ���裺ֱ��Ϊl�ķ���Ϊ��y��![]() x+4��
x+4��
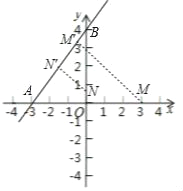
ֱ����x�ᡢy�ύ�������ֱ�Ϊ����3��0������0��4����tan��M��AM��![]() ��
��
����M��M��M��ֱ��l����M��MΪM��ֱ��l�ľ��룬
M��M��MA sin��M��AM��6��![]() ��
��![]() ��
��
��������ã���N��ֱ��l�·�ʱ��
N��N��2��BN��![]() ��
��![]() ��
��
��a��4��![]() ��
��![]() ��
��
��N��ֱ��l�Ϸ�ʱ��a����a��4+ ![]() ��
��![]() ��
��
��a��![]() ��
��![]() ��
��
��3����G��ԭ���·�ʱ��b����3��
��G��ԭ���Ϸ�ʱ��![]() ��
��
�����ã�x4+��1��2b��x2+b2��9��0��
������1��2b��2��4��b2��9����0��
��ã�b��![]() ��
��
��b����3��![]() ��
��


 ��ǰ����ϵ�д�
��ǰ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ���ھ���ABCD��.��O�ڱ�AB�ϣ���AOC=��BOD.��֤��AO=OB.
��2����ͼ��AB��![]() ��ֱ����PA��
��ֱ����PA��![]() �����ڵ�A��OP��
�����ڵ�A��OP��![]() �ཻ�ڵ�C������CB����OPA=40�������ABC�Ķ���.
�ཻ�ڵ�C������CB����OPA=40�������ABC�Ķ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ ![]() ��y��ax2 ���㣨2��2��
��y��ax2 ���㣨2��2��
(1)ֱ��д�������ߵĽ���ʽ��
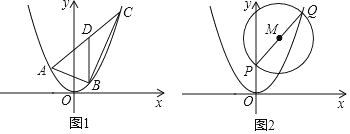
(2)��ͼ����ABC ���������㶼��������![]() �ϣ��ұ� AC ���ڵ�ֱ�߽���ʽΪy��x+b���� AC ���ϵ����� BD ƽ���� y �ᣬ��
�ϣ��ұ� AC ���ڵ�ֱ�߽���ʽΪy��x+b���� AC ���ϵ����� BD ƽ���� y �ᣬ��![]() ��ֵ��
��ֵ��
(3)��ͼ���� P ������Ϊ��0��2������ Q Ϊ��������![]() ��һ���㣬�� PQ Ϊֱ������M��ֱ�� y��t ���M �ཻ�� H��K �����Ƿ����ʵ�� t��ʹ�� HK �ij���Ϊ��ֵ�������ڣ���� HK �ij��ȣ��������ڣ���˵�����ɣ�
��һ���㣬�� PQ Ϊֱ������M��ֱ�� y��t ���M �ཻ�� H��K �����Ƿ����ʵ�� t��ʹ�� HK �ij���Ϊ��ֵ�������ڣ���� HK �ij��ȣ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+3x+c����A����1��0����B��4��0�����㣬��y�ύ�ڵ�C��
��1���������ߵĽ���ʽ��
��2������P�ڵ�һ�����������ϣ��ҵ�P�ĺ�����Ϊt������P��x�������߽�ֱ��BC�ڵ�Q�����߶�PQ�ij�Ϊm����m��t֮��ĺ�����ϵʽ�������m�����ֵ��
��3����x�����Ƿ���ڵ�E��ʹ�Ե�B��C��EΪ�����������Ϊ���������Σ�������ڣ�ֱ��д��E�����ꣻ��������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������С����Ƶġ��������ε�һ���������ö���Աߵ�ƽ���ߡ��ij߹���ͼ���̣�
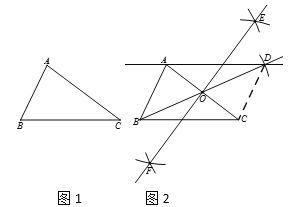
��֪����ͼ1����ABC��
������ֱ��AD��ʹAD��BC��
��������ͼ2��
�ٷֱ��Ե�A��CΪԲ�ģ��Դ���![]() ACΪ�뾶�������������ڵ�E��F��
ACΪ�뾶�������������ڵ�E��F��
����ֱ��EF����AC�ڵ�O��
��������BO��������BO�Ͻ�ȡOD��B��D���غϣ���ʹ��OD = OB��
����ֱ��AD��
�� ֱ��AD������������ƽ���ߣ�
����С����Ƶij߹���ͼ���̣���������֤����
֤��������CD��
����A =OC��OB=OD��
���ı���ABCD��ƽ���ı�����_______________________�������������ݣ���
��AD��BC��__________________________________�������������ݣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪y��x�ĺ������Ա���x��ȡֵ��Χ��![]() ���±���y��x�ļ����Ӧֵ��
���±���y��x�ļ����Ӧֵ��

С������ѧϰ�����ľ��飬����������������ӳ����y��x֮��ı仯���ɣ��Ըú�����ͼ�������ʽ�����̽����������С����̽�����̣��뽫�䲹��������
��1����ͼ����ƽ��ֱ������ϵxOy�У���������ϱ��и����ӦֵΪ����ĵ㣮��������ĵ㣬�����ú�����ͼ��
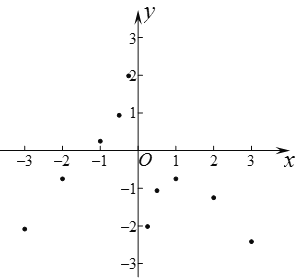
��2�����ݻ����ĺ���ͼ��д����
��![]() ʱ����Ӧ�ĺ���ֵyԼΪ �������ȷ��0.01����
ʱ����Ӧ�ĺ���ֵyԼΪ �������ȷ��0.01����
�ڸú�����һ�����ʣ� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������10�֣���ij����֯�Ĵ�����ҵ�ݳ���У������幺����Ʊʵ���Żݣ�������ԭ��Ʊ�ۻ�����ÿ�Ž���80Ԫ��������ԭ��Ʊ���軨��6000Ԫ�������Ʊ����������ֻ������4800Ԫ��
��1����ÿ����Ʊԭ����Ʊ�ۣ�
��2������ʵ����������֯��λ�������ڸ��˹�ƱҲ��ȡ�Żݴ�ʩ��ԭ��Ʊ�۾����������ν��ۺ�Ϊ324Ԫ����ƽ��ÿ�ν��۵İٷ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������9�֣�
Ϊ�˿���ס������ֳ�����С�����߳���״�����ִ��и������ȡ6�꣬��������ǵ���ߣ���λ��cm�����±���ʾ��
�� | 63 | 66 | 63 | 61 | 64 | 61 |
�� | 63 | 65 | 60 | 63 | 64 | 63 |
��1����ֱ��������������ݵķ������˱Ƚ�����С�����߳��ƱȽ����룿
��2���ֽ���������С������Ʒ���ӽ����飬��ӱ��ڵļס�������С���У��������ȡһ�������ԣ���Ԥ���������״�����������б�������״ͼ�ķ�����������ȡ���������С�����ǡ�ö����ڸ���ƽ����ߵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Сǿ�ﳵ�Ӽҵ�ѧУҪ����һ�������º����µ�·�������·��Сǿ�ﳵ�ľ���s(ǧ��)���ﳵ��ʱ��t�����ӣ�֮��ĺ�����ϵ��ͼ��ʾ�������ͼ����Ϣ�ش��������⣺
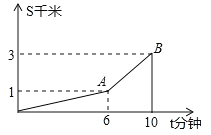
(1)СǿȥѧУʱ����·�� ǧ�ף�
(2)Сǿ���µ��ٶ�Ϊ ǧ��/���ӣ�
(3)��Сǿ�ؼ�ʱ��ԭ·���أ������µ��ٶȲ��䣬���µ��ٶ�Ҳ���䣬��ô�ؼ��ﳵ�����·��ʱ���� ����.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com