
【题目】如图,抛物线y=ax2+3x+c经过A(﹣1,0),B(4,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)若点P在第一象限的抛物线上,且点P的横坐标为t,过点P向x轴作垂线交直线BC于点Q,设线段PQ的长为m,求m与t之间的函数关系式,并求出m的最大值;
(3)在x轴上是否存在点E,使以点B,C,E为顶点的三角形为等腰三角形?如果存在,直接写出E点坐标;如果不存在,请说明理由.

【答案】(1)y=﹣x2+3x+4;(2)m=﹣t2+4t(0<t<4),m的最大值为4;(3)存在,E(﹣4,0)或(0,0)或(4﹣4![]() ,0).
,0).
【解析】
(1)由点A、B的坐标利用待定系数法即可求出抛物线的解析式;
(2)将x=0代入抛物线解析式中可求出点C的坐标,根据点B、C的坐标利用待定系数法即可求出直线BC的解析式,由点P的横坐标为t,即可找出点P、Q的坐标,由此即可用含t的代数式表示出PQ的长度,再利用二次函数的性质即可解决最值问题;
(3)①由CO⊥x轴、QD⊥x轴、∠QBD=∠CBO,即可得出△BQD∽△BCO,即存在点E(0,0)使得△BQD∽△BCE;②过点C作EC⊥BC交x轴于点E,由EC⊥BC、QD⊥x轴、∠QBD=∠CBO,即可得出△BQD∽△BEC,再根据点B、C的坐标即可得出∠CBO=45°,利用等腰直角三角形的性质即可得出此时点E的坐标.综上即可得出结论.
(1)∵抛物线y=ax2+3x+c经过A(﹣1,0),B(4,0),
把A、B两点坐标代入上式,解得:a=﹣1,c=4,
故:抛物线y=﹣x2+3x+4;
(2)∵将x=0代入抛物线的解析式得:y=4,∴C(0,4),
把将B(4,0),C(0,4)代入抛物线方程,
解得:直线BC的解析式为:y=﹣x+4.
过点P作x的垂线PQ,如图所示:

∵点P的横坐标为t,∴P(t,﹣t2+3t+4),Q(t,﹣t+4).
∴PQ=﹣t2+3t+4﹣(﹣t+4)=﹣t2+4t.
∴m=﹣t2+4t=﹣(t﹣2)2+4(0<t<4).
∴当t=2时,m的最大值为4;
(3)存在.如图所示:
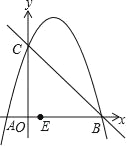
当EC=BE时,E在原点O,此时点E(0,0),
当BC=CE时,E在点B关于y轴对称点,此时点E(﹣4,0),
当BC=BE时,BE=4![]() ,此时E(4﹣4
,此时E(4﹣4![]() ,0)
,0)
即:E(﹣4.0)或(0,0)或(4﹣4![]() ,0).
,0).


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 边上一个动点,过点
边上一个动点,过点![]() 作直线
作直线![]() ,设
,设![]() 交
交![]() 的平分线于点
的平分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() .
.
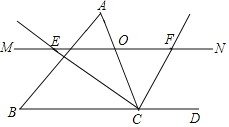
(1)探究![]() 与
与![]() 的数量关系并加以证明;
的数量关系并加以证明;
(2)当点![]() 运动到
运动到![]() 上的什么位置时,四边形
上的什么位置时,四边形![]() 是矩形,请说明理由;
是矩形,请说明理由;
(3)在(2)的基础上,![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是正方形?为什么?
是正方形?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量校园内一棵大树的高度,学校数学应用实践小组做了如下的探索:根据光的反射定律,利用一面镜子和一根皮尺,设计了如图的测量方案,把镜子放在离树(AB)8.7m的点E处,然后沿直线BE后退到点D,这时恰好在镜子里看到树顶点A,再用皮尺测量得DE=2.7m,观察者眼睛距地面的高CD=1.6m,请你计算树(AB)的高度.(精确到0.1m)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙走完全程用了30分钟;③乙用12分钟追上甲;④乙到达终点时,甲离终点还有360米;其中正确的结论有( )
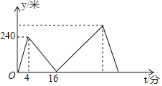
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】瓦子街是上杭城关老城区改造的商业文化购物步行街,瓦子街某商场经营的某个品牌童装,购进时的单价是60元,根据市场调查,在一段时间内,销售单价是80元时,销售量是200件,销售单价每降低1元,就可多售出20件.
![]() 求出销售量
求出销售量![]() 件
件![]() 与销售单价
与销售单价![]() 元
元![]() 之间的函数关系式;
之间的函数关系式;
![]() 求出销售该品牌童装获得的利润
求出销售该品牌童装获得的利润![]() 元
元![]() 与销售单价
与销售单价![]() 元
元![]() 之间的函数关系式;
之间的函数关系式;
![]() 若童装厂规定该品牌童装的销售单价不低于76元且不高于80元,则商场销售该品牌童装获得的最大利润是多少?
若童装厂规定该品牌童装的销售单价不低于76元且不高于80元,则商场销售该品牌童装获得的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:点Q到图形W上每一个点的距离的最小值称为点Q到图形W的距离.
例如,如图1,正方形ABCD满足A(1,0),B(2,0),C(2,1),D(1,1),那么点O(0,0)到正方形ABCD的距离为1.
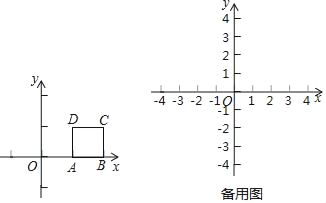
(1)如果⊙P是以(3,4)为圆心,2为半径的圆,那么点O(0,0)到⊙P的距离为 ;
(2)①求点M(3,0)到直线了y=![]() x+4的距离:
x+4的距离:
②如果点N(0,a)到直线y=![]() x+4的距离为2,求a的值;
x+4的距离为2,求a的值;
(3)如果点G(0,b)到抛物线y=x2的距离为3,请直接写出b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线的表达式是y=ax2+(1﹣a)x+1﹣2a(a为不等于0的常数),上述抛物线无论a为何值始终经过定点A和定点B;A为x轴上的点,B为第一象限内的点.
(1)请写出A,B两点的坐标:A( ,0);B( , );
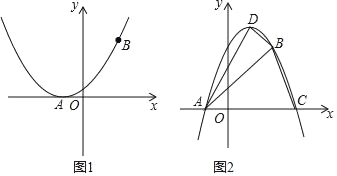
(2)如图1,当抛物线与x轴只有一个公共点时,求a的值;
(3)如图2,当a<0时,若上述抛物线顶点是D,与x轴的另一交点为点C,且点A,B,C,D中没有两个点相互重合.
求:①△ABC能否是直角三角形,为什么?
②若使得△ABD是直角三角形,请你求出a的值.(求出1个a的值即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com