
����Ŀ����֪�����ߵı���ʽ��y=ax2+��1��a��x+1��2a��aΪ������0�ij���������������������aΪ��ֵʼ�վ�������A�Ͷ���B��AΪx���ϵĵ㣬BΪ��һ�����ڵĵ㣮
��1����д��A��B��������꣺A���� ����0����B���� ������ ������
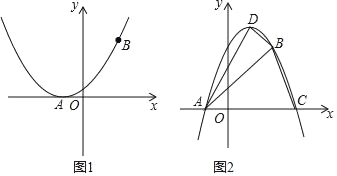
��2����ͼ1������������x��ֻ��һ��������ʱ����a��ֵ��
��3����ͼ2����a��0ʱ�������������߶�����D����x�����һ����Ϊ��C���ҵ�A��B��C��D��û����������غϣ�
�١�ABC�ܷ���ֱ�������Σ�Ϊʲô��
����ʹ�á�ABD��ֱ�������Σ��������a��ֵ�������1��a��ֵ���ɣ�
���𰸡���1����1��2��3����2��a=![]() ����3����a=��
����3����a=��![]() ����a=��1��
����a=��1��
��������
��1��y=ax2+��1-a��x+1-2a=a��x2-x-2��+x+1������x2-x-2��=0ʱ������aΪ��ֵʼ�վ�������A�Ͷ���B��������⣻
��2������������x��ֻ��һ��������ʱ����=0��������⣻
��3����A��-1��0������C��x��0����AB���ڵ�ֱ�ߵ�k1ֵΪ1��BC���ڵ�ֱ�ߵ�k2ֵΪ��![]() =3a����k1k2=-1������⣻���裺��ABD=90�����裺D��m��n��������Τ�ﶨ���ã�m2=-
=3a����k1k2=-1������⣻���裺��ABD=90�����裺D��m��n��������Τ�ﶨ���ã�m2=-![]() ����m=-
����m=-![]() ����y=ax2+��1-a��x+1-2a֪��m=
����y=ax2+��1-a��x+1-2a֪��m=![]() ������-
������-![]() =
=![]() ��������⣮
��������⣮
�⣺��1��y=ax2+��1��a��x+1��2a=a��x2��x��2��+x+1��
����x2��x��2��=0ʱ������aΪ��ֵʼ�վ�������A�Ͷ���B��
��x=��1��2����A����1��0����B��2��3����
�ʣ����ǩ�1��2��3��
��2������������x��ֻ��һ��������ʱ����=0��
������1��a��2��2a��1��2a��=0����ã�a=![]() ��
��
��3����A����1��0������C��x��0����
��Τ�ﶨ������1x=![]() ����C��
����C��![]() ��0����
��0����
AB���ڵ�ֱ�ߵ�k1ֵΪ1��
BC���ڵ�ֱ�ߵ�k2ֵΪ��![]() =3a��
=3a��
��k1k2=��1ʱ��AB��BC����ã�a=��![]() ��
��
���裺��ABD=90�㣬
��ֱ��BD����ֱ�߷��̵�k=��1����ֱ�߷���Ϊ��y=��x+5��
��ֱ��BD���ڵķ�������κ��������ã�
ax2+��2��a��x����4+2a��=0��
�裺D��m��n������B��2��3��
��Τ�ﶨ���ã�m2=��![]() ����m=��
����m=��![]() ��
��
��y=ax2+��1��a��x+1��2a֪��m=![]() ��
��
������![]() =
=![]() ��
��
��ã�a=��1��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+3x+c����A����1��0����B��4��0�����㣬��y�ύ�ڵ�C��
��1���������ߵĽ���ʽ��
��2������P�ڵ�һ�����������ϣ��ҵ�P�ĺ�����Ϊt������P��x�������߽�ֱ��BC�ڵ�Q�����߶�PQ�ij�Ϊm����m��t֮��ĺ�����ϵʽ�������m�����ֵ��
��3����x�����Ƿ���ڵ�E��ʹ�Ե�B��C��EΪ�����������Ϊ���������Σ�������ڣ�ֱ��д��E�����ꣻ��������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������9�֣�
Ϊ�˿���ס������ֳ�����С�����߳���״�����ִ��и������ȡ6�꣬��������ǵ���ߣ���λ��cm�����±���ʾ��
�� | 63 | 66 | 63 | 61 | 64 | 61 |
�� | 63 | 65 | 60 | 63 | 64 | 63 |
��1����ֱ��������������ݵķ������˱Ƚ�����С�����߳��ƱȽ����룿
��2���ֽ���������С������Ʒ���ӽ����飬��ӱ��ڵļס�������С���У��������ȡһ�������ԣ���Ԥ���������״�����������б�������״ͼ�ķ�����������ȡ���������С�����ǡ�ö����ڸ���ƽ����ߵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y1=kx+n��k��0������κ���y2=ax2+bx+c��a��0����ͼ���ཻ��A����1��5����B��9��2�����㣬�����x�IJ���ʽkx+n��ax2+bx+c�Ľ⼯Ϊ��������

A. ��1��x��9 B. ��1��x��9 C. ��1��x��9 D. x����1��x��9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Բ����ˮ����ԭ�л�ˮ��ˮƽ���CD=20cm��ˮ��GF=2cm����ˮ������2cm��EG=2cm�������ʱˮ���
ABΪ���٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
�У�![]() ��CD�Ǹߣ�BEƽ�֡�ABC��CD�ڵ�E��EF��AC��AB�ڵ�F����BC�ڵ�G���ڽ��ۣ�(1)
��CD�Ǹߣ�BEƽ�֡�ABC��CD�ڵ�E��EF��AC��AB�ڵ�F����BC�ڵ�G���ڽ��ۣ�(1) ![]()
![]() ��(2)
��(2) ![]() ��(3)
��(3)![]() ��(4)
��(4) ![]() �У�һ����������( )
�У�һ����������( )
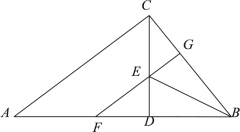
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Сǿ�ﳵ�Ӽҵ�ѧУҪ����һ�������º����µ�·�������·��Сǿ�ﳵ�ľ���s(ǧ��)���ﳵ��ʱ��t�����ӣ�֮��ĺ�����ϵ��ͼ��ʾ�������ͼ����Ϣ�ش��������⣺
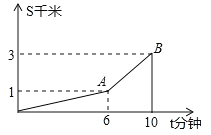
(1)СǿȥѧУʱ����·�� ǧ�ף�
(2)Сǿ���µ��ٶ�Ϊ ǧ��/���ӣ�
(3)��Сǿ�ؼ�ʱ��ԭ·���أ������µ��ٶȲ��䣬���µ��ٶ�Ҳ���䣬��ô�ؼ��ﳵ�����·��ʱ���� ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��O��ֱ��AB�ij�Ϊ10����AC�ij�Ϊ5����ACB��ƽ���߽�O�ڵ�D.

��1������ADC�Ķ�����
��2������BD�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ��� y��ax+bx+c��a��0����ͼ����ͼ��ʾ��A���� 1��3���������ߵĶ��㣬�����½�������ȷ���ǣ� ��
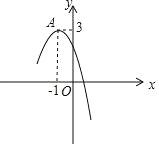
A. a��0��b��0��c��0
B. 2a+b��0
C. �� x��0 ʱ��y �� x ���������С
D. ax2+bx+c��3��0
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com