
【题目】如图,在![]() 中,
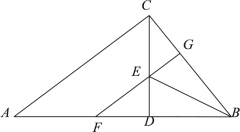
中,![]() ,CD是高,BE平分∠ABC交CD于点E,EF∥AC交AB于点F,交BC于点G.在结论:(1)
,CD是高,BE平分∠ABC交CD于点E,EF∥AC交AB于点F,交BC于点G.在结论:(1) ![]()
![]() ;(2)
;(2) ![]() ;(3)
;(3)![]() ;(4)
;(4) ![]() 中,一定成立的有( )
中,一定成立的有( )
A.1个B.2个C.3个D.4个
【答案】B
【解析】
根据两直线平行,同旁内角互补求出∠CGE=∠BCA=90°,然后根据等角的余角相等即可求出∠EFD=∠BCD;只有△ABC是等腰直角三角形时AD=CD,CG=EG;利用“角角边”证明△BCE和△BFE全等,然后根据全等三角形对应边相等可得BF=BC.
∵EF∥AC,∠BCA=90°,
∴∠CGE=∠BCA=90°,
∴∠BCD+∠CEG=90°,
又∵CD是高,
∴∠EFD+∠FED=90°,
∵∠CEG=∠FED(对顶角相等),
∴∠EFD=∠BCD,故(1)正确;
只有∠A=45°,即△ABC是等腰直角三角形时,AD=CD,CG=EG而立,故(2)(3)不一定成立,错误;
∵BE平分∠ABC,
∴∠EBC=∠EBF,
在△BCE和△BFE中,
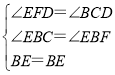 ,
,
∴△BCE≌△BFE(AAS),
∴BF=BC,故(4)正确,
综上所述,正确的有(1)(4)共2个.
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某公司技术人员用“沿直线AB折叠检验塑胶带两条边缘线a、b是否互相平行”.
(1)如图1,测得∠1=∠2,可判定a∥b吗?请说明理由;
(2)如图2,测得∠1=∠2,且∠3=∠4,可判定a∥b吗?请说明理由;
(3)如图3,若要使a∥b,则∠1与∠2应该满足什么关系式?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市郊外景区内一条笔直的公路a经过三个景点A、B、C,景区管委会又开发了风景优美的景点D,经测量景点D位于景点A的北偏东30°方向8km处,位于景点B的正北方向,还位于景点C的北偏西75°方向上,已知AB=5km.

(1)景区管委会准备由景点D向公路a修建一条距离最短的公路,不考虑其它因素,求出这条公路的长;(结果精确到0.1km)
(2)求景点C与景点D之间的距离.(结果精确到1km)
(参考数据:![]() =1.73,
=1.73,![]() =2.24,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73.)
=2.24,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按![]() 元销售时,每天可销售
元销售时,每天可销售![]() 个;若销售单价每降低元,每天可多售出
个;若销售单价每降低元,每天可多售出![]() 个.已知每个玩具的固定成本为
个.已知每个玩具的固定成本为![]() 元,问这种玩具的销售单价为多少元时,厂家每天可获利润
元,问这种玩具的销售单价为多少元时,厂家每天可获利润![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD, ![]() ,
,![]() .求
.求![]() 度数.
度数.

小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得![]() _______.
_______.
问题迁移:如图3,AD∥BC,点P在射线OM上运动, ![]() ,
, ![]() .
.
(1)当点P在A、B两点之间运动时, ![]() 、
、![]() 、
、![]() 之间有何数量关系?请说明理由.
之间有何数量关系?请说明理由.
(2)如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出![]() 、
、![]() 、
、![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
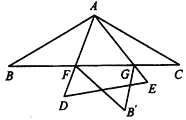
【题目】如图, ![]() 中,
中, ![]() ,
, ![]() =120°,以
=120°,以![]() 为一个顶点的等边三角形
为一个顶点的等边三角形![]() 绕点A在
绕点A在![]() 内旋转,
内旋转, ![]() 、
、![]() 所在的直线与
所在的直线与![]() 边分别交于点
边分别交于点![]() 、
、![]() ,若点
,若点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,当
,当![]() 是以点
是以点![]() 为直角顶点的直角三角形时,
为直角顶点的直角三角形时, ![]() 的长为__
的长为__
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC.
(1)求证:AD=EC;
(2)当∠BAC=Rt∠时,求证:四边形ADCE是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com