
【题目】如图, ![]() 中,
中, ![]() ,
, ![]() =120°,以
=120°,以![]() 为一个顶点的等边三角形
为一个顶点的等边三角形![]() 绕点A在
绕点A在![]() 内旋转,
内旋转, ![]() 、
、![]() 所在的直线与
所在的直线与![]() 边分别交于点
边分别交于点![]() 、
、![]() ,若点
,若点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,当
,当![]() 是以点
是以点![]() 为直角顶点的直角三角形时,
为直角顶点的直角三角形时, ![]() 的长为__
的长为__
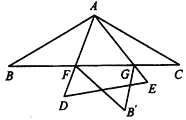
【答案】![]()
【解析】试题解析:作AH⊥BC于H,如图1,
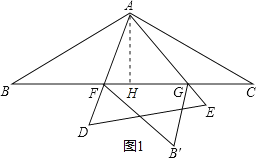
∵AB=AC=4,∠BAC=120°,
∴∠B=30°,BH=CH,
在Rt△ABH中,AH=![]() AB=2,BH=
AB=2,BH=![]() AH=2
AH=2![]() ,
,
∴BC=2BH=4![]() ,
,
把△ACG绕点A顺时针旋转120°得到△ABG′,连结FG′、AB′,如图2,则BG′=CG,AG=AG,∠ABG′=∠C=30°,∠1=∠BAG′,

∴∠FBG′=60°,
∵∠FAG=60°,
∴∠1+∠2=60°,
∴∠FAG′=60°,
在△AFG和△AFG′中,
 ,
,
∴△AFG≌△AFG′,
∴FG=FG′,
∵点B关于直线AD的对称点为B′,
∴FB=FB′,AB=AB′,∠2=∠3,
而∠3+∠4=60°,∠1+∠2=60°,
∴∠1=∠4,
而AC=AB=AB′,
∴△AB′G与△ACG关于AG对称,
∴GB′=GC,
∴GB′=BG′,
在△FB′G和△FBG′中,
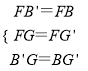 ,
,
∴△FB′G≌△FBG′,
∴∠FGB′=∠BG′F=90°,
在Rt△BFG′中,∵∠FBG′=60°,
∴BG′=![]() BF,FG′=
BF,FG′=![]() BF,
BF,
∴CG=![]() BF,FG=
BF,FG=![]() BF,
BF,
∴BF+![]() BF+
BF+![]() BF=BC=4
BF=BC=4![]() ,
,
∴BF=4![]() -4.
-4.
故答案为4![]() -4.
-4.


科目:初中数学 来源: 题型:
【题目】李大爷以每千克2.1元的价格批发了一批南瓜到镇上出售,为了方便,他带了一些零钱备用,他先按市场价售出一些后,由于滞销,然后他每千克降低1.6元将剩余部分全部售出.他手中持有的钱数y元(含备用零钱)与售出南瓜千克数x的关系如图所示,下列说法中正确的有( )
①李大爷自带的零钱是50元
②降价前他每千克南瓜出售的价格是4.1元
③这批南瓜一共有160千克
④李大爷销售这批南瓜一共赚了194元

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
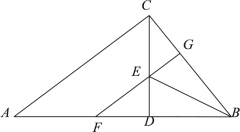
【题目】如图,在![]() 中,
中,![]() ,CD是高,BE平分∠ABC交CD于点E,EF∥AC交AB于点F,交BC于点G.在结论:(1)
,CD是高,BE平分∠ABC交CD于点E,EF∥AC交AB于点F,交BC于点G.在结论:(1) ![]()
![]() ;(2)
;(2) ![]() ;(3)
;(3)![]() ;(4)
;(4) ![]() 中,一定成立的有( )
中,一定成立的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD.
(1)用直尺和圆规作出么ABC的平分线BE,交AD的延长线于点E,交DC于点F(保留作图痕迹,不写作法);
(2)求证:△ABE是等腰三角形;
(3)在(1)中所得图形中,除△ABE外,请你写出其他的等腰三角形.(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,放在平面直角坐标系中的正方形ABCD的边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(如图,它有四个顶点,各顶点数分别是1、2、3、4),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的点数作为直角坐标系中点P的坐标(第一次的点数为横坐标,第二次的点数为纵坐标).
(1)求点P落在正方形面上(含边界,下同)的概率;
(2)将正方形ABCD平移数个单位,是否存在一种平移,使点P落在正方形面上的概率为![]() ?若存在,指出其中的一种平移方式;若不存在,说明理由.
?若存在,指出其中的一种平移方式;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解外来务工子女就学情况,某校对七年级各班级外来务工子女的人数情况进行了统计,发现各班级中外来务工子女的人数有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅统计图:
(1)求该校七年级平均每个班级有多少名外来务工子女?并将该条形统计图补充完整;
(2)学校决定从只有2名外来务工子女的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名外来务工子女来自同一个班级的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖用的签字笔可在甲、乙两个商店买到.已知两个商店的标价都是每支签字笔2元.但甲商店的优惠条件是:购买10支以上,从第11支开始按标价的7折卖;乙商店的优惠条件是:从第1支开始就按标价的8.5折卖.
(1)小颖要买20支签字笔,到哪个商店购买较省钱?
(2)小颖现有40元,最多可买多少支签字笔?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,GD=2CG,连接BG、DE,DE和FG相交于点O.下列结论:①△BCG≌△DCE;②BG⊥DE;③![]() =
=![]() ;④4S△EFO=S△DGO.其中正确的结论有( )
;④4S△EFO=S△DGO.其中正确的结论有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
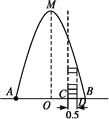
【题目】如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C处(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4 m,AC=3 m,网球飞行最大高度OM=5 m,圆柱形桶的直径为0.5 m,高为0.3 m(网球的体积和圆柱形桶的厚度忽略不计).
(1)如果竖直摆放5个圆柱形桶时,网球能不能落入桶内?
(2)当竖直摆放圆柱形桶多少个时,网球可以落入桶内?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com