
【题目】(操作体验)
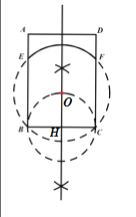
如图①,已知线段AB和直线l,用直尺和圆规在l上作出所有的点P,使得∠APB=30°.

如图②,小明的作图方法如下:
第一步:分别以点A、B为圆心,AB长为半径作弧,两弧在AB上方交于点O;
第二步:连接OA、OB;
第三步:以O为圆心,OA长为半径作⊙O,交l于P1,P2.
所以图中P1,P2即为所求的点.
(1) 在图②中,连接P1A,P1 B,说明∠A P1B=30°;
(方法迁移)
(2)如图③,用直尺和圆规在矩形ABCD内作出所有的点P,使得∠BPC=45°.
(不写作法,保留作图痕迹)

(深入探究)
(3)已知矩形ABCD,BC=2,AB=m,P为AD边上的点,若满足∠BPC=45°的点P恰有两个,则m的取值范围为 .
(4)已知矩形ABCD,AB=3,BC=2,P为矩形ABCD内一点,且∠BPC=135°,若点P绕点A逆时针旋转90°到点Q,则PQ的最小值为 .
【答案】(1)30°;(2)详见解析;(3)2≤m<![]() +1;(4)
+1;(4)![]() ―2.
―2.
【解析】
(1)根据作图可知OA=OB=AB,得到△OAB是等边三角形,根据等边三角形的性质有∠AOB=60°,根据圆周角定理即可求解.
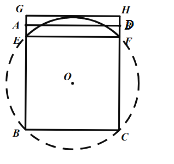
(2)第一步:分别以点B、C为圆心,以大于![]() BC长为半径作弧,作出BC的垂直平分线,与BC交于点H,
BC长为半径作弧,作出BC的垂直平分线,与BC交于点H,
第二步:以点H为圆心,以HB长为半径作圆,与BC的垂直平分线交于点O;
第三步:以O为圆心,OB长为半径作⊙O,交AB交于点E,与CD交于点F, 弧![]() 上所有的点即为所求的点(不含点E、F).
上所有的点即为所求的点(不含点E、F).
(3)当![]() 时,满足∠BPC=45°的点P恰有两个,再求出满足∠BPC=45°的点P变为1个时的临界值,即可求解.
时,满足∠BPC=45°的点P恰有两个,再求出满足∠BPC=45°的点P变为1个时的临界值,即可求解.
(4)按照(2)的作图步骤,则点P在以劣弧BC上(不包含点B,C),根据等腰直角三角形的性质可得![]() 当AP最小时,PQ取得最小值,当点A,P,O在同一条直线上时,AP最小,即图中的AE,求出AE,即可求解.
当AP最小时,PQ取得最小值,当点A,P,O在同一条直线上时,AP最小,即图中的AE,求出AE,即可求解.
(1)解:由作法可知:OA=OB=AB,
∴△OAB是等边三角形,
∴∠AOB=60°.
∴∠AP1B=30°.
(2)如图,弧![]() 上所有的点即为所求的点(不含点E、F).
上所有的点即为所求的点(不含点E、F).
(3)如图:只要![]() 即可,
即可,
当![]() 时,满足∠BPC=45°的点P恰有两个,
时,满足∠BPC=45°的点P恰有两个,
满足∠BPC=45°的点P变为1个时,即到GH的位置时,
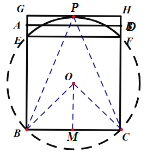
过点![]() 作
作![]() 于点M,
于点M,
![]()
![]()
![]()
![]()
此时:![]()
则![]() 的取值范围是:
的取值范围是:![]()
故答案为:![]()
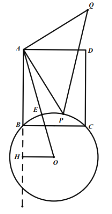
(4)按照(2)的作图步骤,则点P在以劣弧BC上(不包含点B,C),如图,
![]()
当AP最小时,PQ取得最小值,当点A,P,O在同一条直线上时,AP最小,即图中的AE,
![]()
![]()
故答案为:![]()


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点A在x轴的正半轴上,菱形ABCD的边长为2,顶点C的坐标为![]() .
.
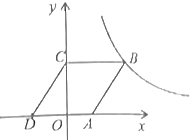
(1)求图像过点B的反比例函数的解析式;
(2)求图像过点A,B的一次函数的解析式;
(3)在第一象限内,当以上所求一次函数的图像在所求反比例函数的图像下方时,请直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
(k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
(1)求反比例函数的解析式及B点的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景
(1)如图1,△ABC中,DE∥BC分别交AB,AC于D,E两点,过点E作EF∥AB交BC于点F.请按图示数据填空:
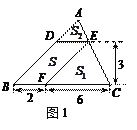
四边形DBFE的面积![]() ,
,
△EFC的面积![]() ,
,
△ADE的面积![]() .
.
探究发现
(2)在(1)中,若![]() ,
,![]() ,DE与BC间的距离为
,DE与BC间的距离为![]() .请证明
.请证明![]() .
.
拓展迁移
(3)如图2,□DEFG的四个顶点在△ABC的三边上,若△ADG、△DBE、△GFC的面积分别为2、5、3,试利用(2)中的结论求△ABC的面积.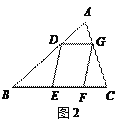
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“特色江苏,美好生活”,第十届江苏省园艺博览会在扬州举行.圆圆和满满同学分析网上关于园博会的信息,发现最具特色的场馆有:扬州园,苏州园,盐城园,无锡园.他们准备周日下午去参观游览,各自在这四个园中任选一个,每个园被选中的可能性相同.
(1)圆圆同学在四个备选园中选中扬州园的概率是 .
(2)用树状图或列表法求出圆圆和满满他们选中同一个园参观的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)当![]() 时,利用根的判别式判断方程根的情况,
时,利用根的判别式判断方程根的情况,
(2)若方程有两个相等的非零实数根,写出一组满足条件的![]() 的值,并求此时方程的根.
的值,并求此时方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
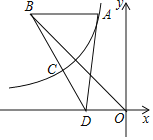
【题目】如图,点A是双曲线y=![]() 上一点,过A作AB∥x轴,交直线y=-x于点B,点D是x轴上一点,连接BD交双曲线于点C,连接AD,若BC:CD=3:2,△ABD的面积为
上一点,过A作AB∥x轴,交直线y=-x于点B,点D是x轴上一点,连接BD交双曲线于点C,连接AD,若BC:CD=3:2,△ABD的面积为![]() ,tan∠ABD=
,tan∠ABD=![]() ,则k的值为( )
,则k的值为( )
A. -![]() B. -3C. -2D.
B. -3C. -2D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程x2+4x﹣9=0时,原方程可变形为( )
A. (x+2)2=1 B. (x+2)2=7 C. (x+2)2=13 D. (x+2)2=19
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com