
����Ŀ������ɫ���գ���������������ʮ�콭��ʡ�ղ����������ݾ���.ԲԲ������ͬѧ�������Ϲ����������Ϣ�����������ɫ�ij����У��������������γ�������.��������������ȥ�ι����������������ĸ�����ѡһ����ÿ����ѡ�еĿ�������ͬ.
��1��ԲԲͬѧ���ĸ���ѡ��ѡ�������ĸ����� .
��2������״ͼ���б������ԲԲ����������ѡ��ͬһ���ι۵ĸ����Ƕ��٣�
 Сѧ��ʱ��ҵȫͨ����ϵ�д�
Сѧ��ʱ��ҵȫͨ����ϵ�д� �����ÿ�ʱѵ��ϵ�д�
�����ÿ�ʱѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
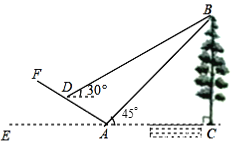
����Ŀ����ͼ��С��Ϊ�˲���С�Ӷ�����BC�ĸ߶ȣ����ڵ�A��ô�������B��������45������б����![]() ����б���ϵ�D���ڴ˴���������˵�B������Ϊ30������б��AF���±�Ϊ1�U2����С���ӵ�A�ߵ���D�Ĺ����У��������ĸ߶�Ϊ____�ף�����BC�ĸ߶�Ϊ____�ף�����������ţ���
����б���ϵ�D���ڴ˴���������˵�B������Ϊ30������б��AF���±�Ϊ1�U2����С���ӵ�A�ߵ���D�Ĺ����У��������ĸ߶�Ϊ____�ף�����BC�ĸ߶�Ϊ____�ף�����������ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ![]() ����ƽ��ֱ�ǽ�����ϵ�У���֪������
����ƽ��ֱ�ǽ�����ϵ�У���֪������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ����.
����.
(1)�������ߵĺ�������ʽ��
(2)��ͼ![]() ��
��![]() �����������ཻ�ڵ�
�����������ཻ�ڵ�![]() ����
����![]() ��ֱ��
��ֱ��![]() �·��������ϵĶ��㣬����
�·��������ϵĶ��㣬����![]() ����
����![]() ��ƽ�е�ֱ����
��ƽ�е�ֱ����![]() ,
,![]() �ֱ��ڵ�
�ֱ��ڵ�![]() ��̽������
��̽������![]() �˶����δ�ʱ���߶�
�˶����δ�ʱ���߶�![]() ��������
��������![]() �����ꣻ
�����ꣻ
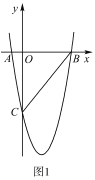
(3)����![]() Ϊ�����ߵĶ��㣬��
Ϊ�����ߵĶ��㣬��![]() �Ǹ��������ϵ�һ�㣬��
�Ǹ��������ϵ�һ�㣬��![]() �ᡢ
�ᡢ![]() ���Ϸֱ��ҵ�
���Ϸֱ��ҵ�![]() ��ʹ�ı���
��ʹ�ı���![]() ���ܳ���С���������
���ܳ���С���������![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() ��3��
��3��![]() ��
��![]() ��1���ڵ�A��1��3��������A��x���ƽ���ߣ��ֱ������������ڵ�B��C�������½��٣�������xȡ��ֵ��
��1���ڵ�A��1��3��������A��x���ƽ���ߣ��ֱ������������ڵ�B��C�������½��٣�������xȡ��ֵ��![]() ��ֵ������������2a��1���۵�x��0ʱ��
��ֵ������������2a��1���۵�x��0ʱ��![]() ��
��![]() ��4����2AB��3AC��������ȷ������______��������ţ�
��4����2AB��3AC��������ȷ������______��������ţ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������ԭ��O��������y��ax2��bx��a��0����x�ύ����һ��A��3��0�����ڵ�һ��������ֱ��y��x���ڵ�B��4��t����
��1�������������ߵı���ʽ��
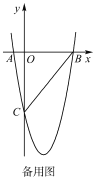
��2����ֱ��OB�·�������������һ��C��������B��O��CΪ����������ε����������C�����ꣻ
��3����ͼ2������M�������������ϣ��ҡ�MBO����ABO���ڣ�2���������£��Ƿ���ڵ�P��ʹ�á�POC�ס�MOB�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������飩
��ͼ�٣���֪�߶�AB��ֱ��l����ֱ�ߺ�Բ����l���������еĵ�P��ʹ�á�APB��30����

��ͼ�ڣ�С������ͼ�������£�
��һ�����ֱ��Ե�A��BΪԲ����AB��Ϊ�뾶������������AB�Ϸ����ڵ�O��
�ڶ���������OA��OB��
����������OΪԲ�ģ�OA��Ϊ�뾶����O����l��P1��P2��
����ͼ��P1��P2��Ϊ����ĵ㣮
��1�� ��ͼ���У�����P1A��P1 B��˵����A P1B��30����
������Ǩ�ƣ�
��2����ͼ�ۣ���ֱ�ߺ�Բ���ھ���ABCD���������еĵ�P��ʹ�á�BPC��45����
����д������������ͼ�ۼ���

������̽����
��3����֪����ABCD��BC��2��AB��m��PΪAD���ϵĵ㣬�������BPC��45���ĵ�Pǡ����������m��ȡֵ��ΧΪ ��
��4����֪����ABCD��AB��3��BC��2��PΪ����ABCD��һ�㣬�ҡ�BPC��135��������P�Ƶ�A��ʱ����ת90������Q����PQ����СֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y=kx+2��x�ᡢy��ֱ��ڵ�A��-1��0���͵�B���뷴��������y=![]() ��ͼ���ڵ�һ�����ڽ��ڵ�C��1��n����
��ͼ���ڵ�һ�����ڽ��ڵ�C��1��n����
��1����k��ֵ��
��2�����������Ľ���ʽ��
��3����x���ϵĵ�D��a��0����ƽ����y���ֱ��l��a��1�����ֱ���ֱ��AB��˫����y=![]() ���ڵ�P��Q����PQ=2QD�����D�����꣮
���ڵ�P��Q����PQ=2QD�����D�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ڡ����ҹ��Ĵ�ͳ�ѽڣ���������гԡ����ӡ���ϰ�ס�����ijʳƷ��Ϊ�˽������ȥ�������Ϻõ������գ��̣�����ɳ���գ��𣩡��������գ��𣩡��������գ��̣������·ֱ���![]() ��ʾ�������ֲ�ͬ��ζ���ӵ�ϲ��������ڽ�ǰ��ij��������������˳������飬��������������Ƴ���������ͳ��ͼ���в��������������������Ϣ�ش�
��ʾ�������ֲ�ͬ��ζ���ӵ�ϲ��������ڽ�ǰ��ij��������������˳������飬��������������Ƴ���������ͳ��ͼ���в��������������������Ϣ�ش�
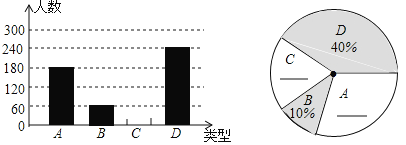
��1�����βμӳ�������ľ����ж����ˣ�
��2����������������ͼ����������
��3������������7000�ˣ�����ư���A�յ�������
��4������������ȫ��ͬ��![]() �ո�һ���������С���������������б�����״ͼ�ķ����������Ե����������Ӷ�����ζ�ĸ��ʡ�
�ո�һ���������С���������������б�����״ͼ�ķ����������Ե����������Ӷ�����ζ�ĸ��ʡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����±���ʾ����A��B��������
��1���� | ��2���� | ��3���� | ��4���� | ���� | ��9���� | ���� | ��n���� | |
A�� | ��6 | ��5 | ��2 | ���� | 58 | ���� | n2��2n��5 | |
B�� | 1 | 4 | 7 | 10 | ���� | 25 | ���� |
��1��A���4�������� ����
��2���ú�n�Ĵ���ʽ��ʾB���n�������� �������������ɣ�
��3�������������У��Ƿ����ͬһ���ϵ���������ȣ���˵����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com