
ЁОЬтФПЁПШчЭМЃЌФГЙЄГЇгы![]() СНЕигаЬњТЗЯрСЌЃЌИУЙЄГЇДг
СНЕигаЬњТЗЯрСЌЃЌИУЙЄГЇДг![]() ЕиЙКТђдВФСЯЃЌжЦГЩВњЦЗЯњЭљ
ЕиЙКТђдВФСЯЃЌжЦГЩВњЦЗЯњЭљ![]() Еи. вбжЊУПЖжНјМлЮЊ600дЊЃЈКЌМгЙЄЗбЃЉЃЌМгЙЄЙ§ГЬжа1ЖждСЯПЩЩњВњВњЦЗ
Еи. вбжЊУПЖжНјМлЮЊ600дЊЃЈКЌМгЙЄЗбЃЉЃЌМгЙЄЙ§ГЬжа1ЖждСЯПЩЩњВњВњЦЗ![]() ЖжЃЌЕБдЄМЦЯњЪлВњЦЗВЛГЌЙ§120ЖжЪБЃЌУПЖжЪлМл1600дЊЃЌГЌЙ§120ЖжЃЌУПдіМг1ЖжЃЌЯњЪлЫљгаВњЦЗЕФМлИёНЕЕЭ2дЊ. ЩшИУЙЄГЇга
ЖжЃЌЕБдЄМЦЯњЪлВњЦЗВЛГЌЙ§120ЖжЪБЃЌУПЖжЪлМл1600дЊЃЌГЌЙ§120ЖжЃЌУПдіМг1ЖжЃЌЯњЪлЫљгаВњЦЗЕФМлИёНЕЕЭ2дЊ. ЩшИУЙЄГЇга![]() ЖжВњЦЗЯњЭљ
ЖжВњЦЗЯњЭљ![]() Еи. ЃЈРћШѓЃНЪлМлЁЊНјМлЁЊдЫЗбЃЉ
Еи. ЃЈРћШѓЃНЪлМлЁЊНјМлЁЊдЫЗбЃЉ
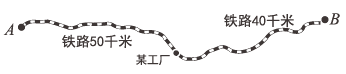

ЃЈ1ЃЉгУ![]() ЕФДњЪ§ЪНБэЪОЙКТђЕФдВФСЯга Жж.
ЕФДњЪ§ЪНБэЪОЙКТђЕФдВФСЯга Жж.
ЃЈ2ЃЉДг![]() ЕиЙКТђдВФСЯВЂМгЙЄжЦГЩВњЦЗЯњЭљ
ЕиЙКТђдВФСЯВЂМгЙЄжЦГЩВњЦЗЯњЭљ![]() ЕиКѓЃЌШєзмдЫЗбЮЊ9600дЊЃЌЧѓ
ЕиКѓЃЌШєзмдЫЗбЮЊ9600дЊЃЌЧѓ![]() ЕФжЕЃЌВЂжБНгаДГіетХњВњЦЗШЋВПЯњЪлКѓЕФзмРћШѓ.
ЕФжЕЃЌВЂжБНгаДГіетХњВњЦЗШЋВПЯњЪлКѓЕФзмРћШѓ.
ЃЈ3ЃЉЯжЙЄГЇЯњЭљ![]() ЕиЕФВњЦЗжСЩй120ЖжЃЌЧвУПЖжЪлМлВЛЕУЕЭгк1440дЊЃЌМЧЯњЭъВњЦЗЕФзмРћШѓЮЊ
ЕиЕФВњЦЗжСЩй120ЖжЃЌЧвУПЖжЪлМлВЛЕУЕЭгк1440дЊЃЌМЧЯњЭъВњЦЗЕФзмРћШѓЮЊ![]() дЊЃЌЧѓ
дЊЃЌЧѓ![]() Йигк
Йигк![]() ЕФКЏЪ§БэДяЪНЃЌМАзюДѓзмРћШѓ.
ЕФКЏЪ§БэДяЪНЃЌМАзюДѓзмРћШѓ.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЕФжЕЮЊ60ЖжЃЌЧветХњВњЦЗШЋВПЯњЪлКѓЕФзмРћШѓЮЊ38400дЊЃЛЃЈ3ЃЉ
ЕФжЕЮЊ60ЖжЃЌЧветХњВњЦЗШЋВПЯњЪлКѓЕФзмРћШѓЮЊ38400дЊЃЛЃЈ3ЃЉ![]() ЃЌЦфзюДѓЕФРћШѓЮЊ96000дЊ
ЃЌЦфзюДѓЕФРћШѓЮЊ96000дЊ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтСаЪНМЦЫуМДПЩЃЛ
ЃЈ2ЃЉИљОнЬтвтСаЗНГЬМДПЩЕУЕННсТлЃЛ
ЃЈ3ЃЉЩшВњЦЗЕФЪлМлЮЊyдЊЃЌИљОнЬтвтКЏЪ§НтЮіЪНЃЌШЛКѓИљОнЖўДЮКЏЪ§ЕФаджЪМДПЩЕУЕННсТлЃЎ
НтЃКЃЈ1ЃЉ![]()
![]()
ЃЈ2ЃЉ![]() ЃЌ
ЃЌ
НтЕУ![]()
змРћШѓЮЊ38400дЊ.
Ыљвд![]() ЕФжЕЮЊ60ЖжЃЌЧветХњВњЦЗШЋВПЯњЪлКѓЕФзмРћШѓЮЊ38400дЊ.
ЕФжЕЮЊ60ЖжЃЌЧветХњВњЦЗШЋВПЯњЪлКѓЕФзмРћШѓЮЊ38400дЊ.
ЃЈ3ЃЉЩшВњЦЗЕФЪлМлЮЊ![]() дЊЃЌгЩЬтвтЕУЃЌ
дЊЃЌгЩЬтвтЕУЃЌ![]()
![]()
ЃН![]()
ЕБ![]() ЪБЃЌВЛдк
ЪБЃЌВЛдк![]() ЗЖЮЇФкЃЌ
ЗЖЮЇФкЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() Ыц
Ыц![]() ЕФдіДѓЖјдіДѓЃЌ
ЕФдіДѓЖјдіДѓЃЌ
ЫљвдЕБ![]() ЪБЃЌ
ЪБЃЌ![]() газюДѓжЕЮЊ96000дЊ.
газюДѓжЕЮЊ96000дЊ.
Д№ЃК![]() Йигк
Йигк![]() ЕФКЏЪ§ЙиЯЕЪНЮЊЃК
ЕФКЏЪ§ЙиЯЕЪНЮЊЃК![]() ЃЌЦфзюДѓЕФРћШѓЮЊ96000дЊ.
ЃЌЦфзюДѓЕФРћШѓЮЊ96000дЊ.


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
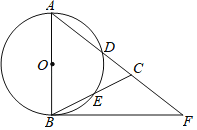
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃНACЃЌвдABЮЊжБОЖЕФЁбOЗжБ№НЛACЁЂBCгкЕуDЁЂEЃЌЕуFдкACЕФбгГЄЯпЩЯЃЌЧвЁЯCBFЃН![]() ЁЯCABЃЎ
ЁЯCABЃЎ
ЃЈ1ЃЉЧѓжЄЃКжБЯпBFЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєABЃН5ЃЌsinЁЯBADЃН![]() ЃЌЧѓADЕФГЄЃЛ
ЃЌЧѓADЕФГЄЃЛ
ЃЈ3ЃЉЪдЬНОПFBЁЂFDЁЂFAжЎМфЕФЙиЯЕЃЌВЂжЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
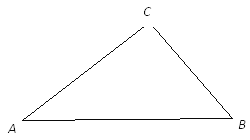
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуDЁЂEЗжБ№дкЁїACDЕФБпABКЭACЩЯЃЌвбжЊDEЁЮBCЃЌDEЃНDBЃЎ
ЃЈ1ЃЉЧыгУжБГпКЭдВЙцдкЭМжаЛГіЕуDКЭЕуEЃЈБЃСєзїЭМКлМЃЃЌВЛвЊЧѓаДзїЗЈЃЉЃЌВЂжЄУїЫљзїЕФЯпЖЮDEЪЧЗћКЯЬтФПвЊЧѓЕФЃЛ
ЃЈ2ЃЉШєABЃН7ЃЌBCЃН3ЃЌЧыЧѓГіDEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧгЩ7ИіЭЌбљДѓаЁЕФе§ЗНЬхАкГЩЕФМИКЮЬхЃЎНЋе§ЗНЬхЂйвЦзпКѓЃЌЫљЕУМИКЮЬхЃЈЁЁЁЁЃЉ
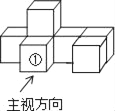
A. жїЪгЭМИФБфЃЌИЉЪгЭМИФБф B. зѓЪгЭМИФБфЃЌИЉЪгЭМИФБф
C. ИЉЪгЭМВЛБфЃЌзѓЪгЭМИФБф D. жїЪгЭМВЛБфЃЌзѓЪгЭМВЛБф
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌЕиУцBDЩЯСНИљЕШГЄСЂжљABЃЌCDжЎМфаќЙввЛИљНќЫЦГЩХзЮяЯпy=![]() x2Љ
x2Љ![]() x+3ЕФЩўзгЃЎ
x+3ЕФЩўзгЃЎ

ЃЈ1ЃЉЧѓЩўзгзюЕЭЕуРыЕиУцЕФОрРыЃЛ
ЃЈ2ЃЉвђЪЕМЪашвЊЃЌдкРыABЮЊ3УзЕФЮЛжУДІгУвЛИљСЂжљMNГХЦ№ЩўзгЃЈШчЭМ2ЃЉЃЌЪЙзѓБпХзЮяЯпF1ЕФзюЕЭЕуОрMNЮЊ1УзЃЌРыЕиУц1.8УзЃЌЧѓMNЕФГЄЃЛ
ЃЈ3ЃЉНЋСЂжљMNЕФГЄЖШЬсЩ§ЮЊ3УзЃЌЭЈЙ§ЕїећMNЕФЮЛжУЃЌЪЙХзЮяЯпF2ЖдгІКЏЪ§ЕФЖўДЮЯюЯЕЪ§ЪМжеЮЊ![]() ЃЌЩшMNРыABЕФОрРыЮЊmЃЌХзЮяЯпF2ЕФЖЅЕуРыЕиУцОрРыЮЊkЃЌЕБ2ЁмkЁм2.5ЪБЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
ЃЌЩшMNРыABЕФОрРыЮЊmЃЌХзЮяЯпF2ЕФЖЅЕуРыЕиУцОрРыЮЊkЃЌЕБ2ЁмkЁм2.5ЪБЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
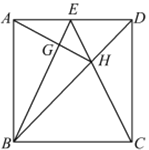
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮ![]() жаЃЌЕу
жаЃЌЕу![]() ЪЧ
ЪЧ![]() БпЕФжаЕуЃЌ
БпЕФжаЕуЃЌ![]() НЛгкЕу
НЛгкЕу![]() ,
,![]() НЛгкЕу
НЛгкЕу![]() ЃЌдђЯТСаНсТлЃКЂй
ЃЌдђЯТСаНсТлЃКЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂм
ЃЛЂм![]() ЃЌЦфжае§ШЗЕФД№АИЪЧ____ЃЎ
ЃЌЦфжае§ШЗЕФД№АИЪЧ____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
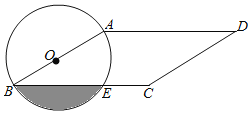
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮABCDжаЃЌABЃМADЃЌЁЯD=30ЁуЃЌCD=4ЃЌвдABЮЊжБОЖЕФЁбOНЛBCгкЕуEЃЌдђвѕгАВПЗжЕФУцЛ§ЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,ФГЫўЙлЙтВуЕФзюЭтбиЕуEЮЊБФМЋЯюФПЕФЦ№ЬјЕу.вбжЊЕуEРыЫўЕФжажсЯпABЕФОрРыOEЮЊ10Уз,ЫўИпABЮЊ123Уз(ABДЙжБЕиУцBC),дкЕиУцCДІВтЕУЕуEЕФбіНЧІС=45Ёу,ДгЕуCбиCBЗНЯђЧАаа40УзЕНДяDЕу,дкDДІВтЕУЫўМтAЕФбіНЧІТ=60Ёу,ЧѓЕуEРыЕиУцЕФИпЖШEF.(НсЙћОЋШЗЕН0.1Уз)

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌЕуOЪЧ
ЃЌЕуOЪЧ![]() ЩЯвЛЕуЃЌвдOЮЊдВаФЃЌ
ЩЯвЛЕуЃЌвдOЮЊдВаФЃЌ![]() ЮЊАыОЖЕФдВЗжБ№НЛ
ЮЊАыОЖЕФдВЗжБ№НЛ![]() гкЕу
гкЕу![]() ЃЌЕуDЪЧЛЁ
ЃЌЕуDЪЧЛЁ![]() ЕФжаЕу.
ЕФжаЕу.
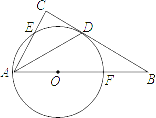
ЃЈ1ЃЉЪдХаЖЯжБЯп![]() гы
гы![]() ЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓЛЁ
ЃЌЧѓЛЁ![]() ЕФГЄЖШЃЈНсЙћБЃСє
ЕФГЄЖШЃЈНсЙћБЃСє![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com