
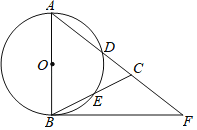
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=![]() ∠CAB.
∠CAB.
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠BAD=![]() ,求AD的长;
,求AD的长;
(3)试探究FB、FD、FA之间的关系,并证明.
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,以点A为圆心、AB的长为半径画弧交AD于点F,再分别以点B,F为圆心、大于![]() BF的长为半径画弧,两弧交于点M,作射线AM交BC于点E,连接EF.下列结论中不一定成立的是( )
BF的长为半径画弧,两弧交于点M,作射线AM交BC于点E,连接EF.下列结论中不一定成立的是( )

A. BE=EFB. EF∥CDC. AE平分∠BEFD. AB=AE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,我市某中学决定根据学生的兴趣爱好组建课外兴趣小组,因此学校随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
(1)学校这次调查共抽取了 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“戏曲”所在扇形的圆心角度数为 ;
(4)设该校共有学生2000名,请你估计该校有多少名学生喜欢书法?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台为了解本地区电视节目的收视情况,对部分市民开展了“你最喜爱的电视节目”的问卷调查(每人只填写一项),根据收集的数据绘制了两幅不完整的统计图(如图所示),根据要求回答下列问题:
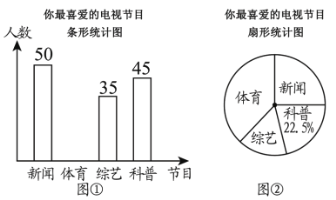
(1)本次问卷调查共调查了________名观众;图②中最喜爱“新闻节目”的人数占调查总人数的百分比为________;
(2)补全图①中的条形统计图;
(3)现有最喜爱“新闻节目”(记为![]() ),“体育节目”(记为
),“体育节目”(记为![]() ),“综艺节目”(记为
),“综艺节目”(记为![]() ),“科普节目”(记为
),“科普节目”(记为![]() )的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用列表或画树状图的方法,求出恰好抽到最喜爱“
)的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用列表或画树状图的方法,求出恰好抽到最喜爱“![]() ”和“
”和“![]() ”两位观众的概率.
”两位观众的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解八年级500名学生的身体素质情况,体育老师从中随机抽取50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出如下频数分布表和频数分布直方图(不完整):
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 |
|
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
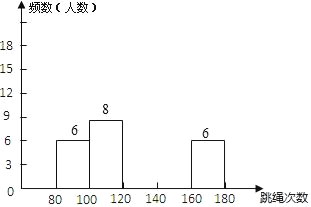
完成下列问题:
(1)请把上面的频数分布表和频数分布直方图补充完整;
(2)这个样本数据的中位数落在第 组;次数在140≤x<160这组的频率为 ;
(3)若八年级学生一分钟跳绳次数(x)达标要求是:x<120不合格;x≥120合格,试问该年级合格的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把1,1,2,3,5,8,13,21,…,这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧 ![]() ,
,![]() ,
,![]() ,…,得到斐波那契螺旋线,然后顺次连结P1P2,P2P3,P3P4,…,得到螺旋折线(如图),已知点P1(0,1),P2(-1,0),P3(0,-1),则该折线上的点P9的坐标为( )
,…,得到斐波那契螺旋线,然后顺次连结P1P2,P2P3,P3P4,…,得到螺旋折线(如图),已知点P1(0,1),P2(-1,0),P3(0,-1),则该折线上的点P9的坐标为( )
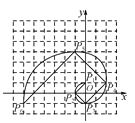
A. (-6,24)B. (-6,25)C. (-5,24)D. (-5,25)
查看答案和解析>>
科目:初中数学 来源: 题型:
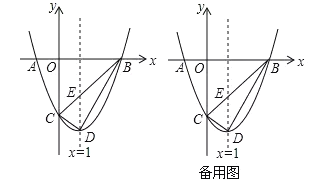
【题目】如图,在平面直角坐标系中,抛物线y=ax2-2x+c的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点A、B的坐标分别为(-1,0),(3,0),点D为抛物线的顶点,抛物线的对称轴与直线BC相交于点E.
(1)求抛物线的解析式和点C的坐标;
(2)点P是直线BC下方的抛物线上一动点,当△PBC的面积最大时,请求出P点的坐标和△PBC的最大面积;
(3)点Q是线段BD上的一动点,将△DEQ沿边EQ翻折得到△![]() ,是否存在点Q使得△
,是否存在点Q使得△![]() 与△BEQ的重叠部分图形为直角三角形?若存在,请直接写出BQ的长,若不存在,请说明理由.
与△BEQ的重叠部分图形为直角三角形?若存在,请直接写出BQ的长,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小丽暑期参加工厂社会实践活动,师傅将他们工作第一周每天生产的合格产品的个数整理成如表两组数据,那么关于他们工作第一周每天生产的合格产品个数,下列说法中正确的是( )
小明 | 2 | 6 | 7 | 7 | 8 |
小丽 | 2 | 3 | 4 | 8 | 8 |
A. 小明的平均数小于小丽的平均数
B. 两人的中位数相同
C. 两人的众数相同
D. 小明的方差小于小丽的方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某工厂与![]() 两地有铁路相连,该工厂从
两地有铁路相连,该工厂从![]() 地购买原材料,制成产品销往
地购买原材料,制成产品销往![]() 地. 已知每吨进价为600元(含加工费),加工过程中1吨原料可生产产品
地. 已知每吨进价为600元(含加工费),加工过程中1吨原料可生产产品![]() 吨,当预计销售产品不超过120吨时,每吨售价1600元,超过120吨,每增加1吨,销售所有产品的价格降低2元. 设该工厂有
吨,当预计销售产品不超过120吨时,每吨售价1600元,超过120吨,每增加1吨,销售所有产品的价格降低2元. 设该工厂有![]() 吨产品销往
吨产品销往![]() 地. (利润=售价—进价—运费)
地. (利润=售价—进价—运费)
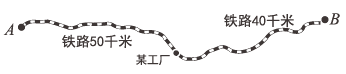

(1)用![]() 的代数式表示购买的原材料有 吨.
的代数式表示购买的原材料有 吨.
(2)从![]() 地购买原材料并加工制成产品销往
地购买原材料并加工制成产品销往![]() 地后,若总运费为9600元,求
地后,若总运费为9600元,求![]() 的值,并直接写出这批产品全部销售后的总利润.
的值,并直接写出这批产品全部销售后的总利润.
(3)现工厂销往![]() 地的产品至少120吨,且每吨售价不得低于1440元,记销完产品的总利润为
地的产品至少120吨,且每吨售价不得低于1440元,记销完产品的总利润为![]() 元,求
元,求![]() 关于
关于![]() 的函数表达式,及最大总利润.
的函数表达式,及最大总利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com