
【题目】如图,已知点D、E分别在△ACD的边AB和AC上,已知DE∥BC,DE=DB.
(1)请用直尺和圆规在图中画出点D和点E(保留作图痕迹,不要求写作法),并证明所作的线段DE是符合题目要求的;
(2)若AB=7,BC=3,请求出DE的长.
【答案】(1)作图见解析;(2)2.1.
【解析】试题分析:(1) ①作∠CBA的平分线交AC于点E ;②作BE的垂直平分线交AB于点D.由线段垂直平分线的性质和角平分线的性质即可得到∠DEB=∠CBE,从而得到结论;
(2)由DE∥BC得到△ADE∽△ABC,再由相似三角形对应边成比例即可得到结论.
试题解析:解:(1)如图:
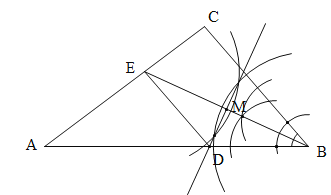
∵BE平分∠ABC,∴∠CBE=∠ABE.∵DM是BE的垂直平分线,∴DE=DB,∴∠DEB=∠DBE,∴∠DEB=∠CBE,∴DE∥BC,DE=DB.
(2) ∵DE∥BC,∴△ADE∽△ABC,∴AD:AB=DE:BC,∴(7-DB):7=DE:3,∴(7-DE):7=DE:3,解得: DE=2.1.


科目:初中数学 来源: 题型:
【题目】规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.当﹣1<x<1时,化简 [x]+(x)+[x)的结果是__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上点A表示-3,点B表示4.
(1)点A与点B之间的距离是 ;
(2)我们知道,在数轴上|a|表示数a所对应的点到原点的距离,你能说明![]() 在数轴上表示的意义吗?
在数轴上表示的意义吗?
(3)在数轴上点P表示的数为x,是否存在这样的点P,使2PA+PB=12?若存在,请求出相应的x;若不存在,请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】股民李明上星期六买进春兰公司股票1000股,每股27元.下表为本周内每日该股票的涨跌情况(单位:元)(注:本周一股票涨跌是在上周六的基础上,用正数记股价比前一日上升数,用负数记股价比前一日下降数)
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
每股涨跌 | +4 | +4.5 | -1 | -2.5 | -6 | +2 |
(1)星期三收盘时,每股是多少元?
(2)本周内最高价是每股多少元?最低价每股多少元?
(3)己知李明买进股票时付了0.15%的手续费,卖出时需付成交额0.15%的手续费和0.1%的交易税,如果李明在星期六收盘前将全部股票卖出,他的收益情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:矩形ABCD中,AB=4,BC=3,点M、N分别在边AB、CD上,直线MN交矩形对角线 AC于点E,将△AME沿直线MN翻折,点A落在点P处,且点P在射线CB上.
(1)如图1,当EP⊥BC时,求CN的长;
(2) 如图2,当EP⊥AC时,求AM的长;
(3) 请写出线段CP的长的取值范围,及当CP的长最大时MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们约定:64 2 2 2 2 2 2可表示成f (6)64,也可表示成g(64)6,
(1)求:f (8) ;
(2)求:g(512);
(3)求:gf (x) (x 为正整数);
(4)f (x y) f (x) f ( y)(x,y 是正整数)成立吗?为什么?
(5)x,y 分别表示若干个2相乘的积,类比④你能写出与 g 相关的等式吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为( )
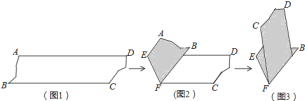
A.120°B.108°C.126°D.114°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为了绿化环境,计划分两次购进A、B两种树苗,第一次分别购进A、B两种树苗30棵和15棵,共花费675元;第二次分别购进A、B两种树苗12棵和5棵,共花费265元.两次购进的A、B两种树苗价格均分别相同.
(1)A、B两种树苗每棵的价格分别是多少元?
解:设A种树苗每棵x元,B种树苗每棵y元
根据题意列方程组,得: ;
解这个方程组,得: ;
答: .
(2)若购买A、B两种树苗共31棵,且购买树苗的总费用不超过320元,则最多可以购买A种树苗多少棵?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com