
【题目】如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线y=![]() (x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD.已知△AOB∽△ACD,相似比为
(x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD.已知△AOB∽△ACD,相似比为![]() .
.
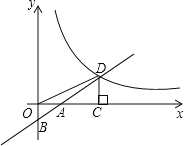
(1)如果b=﹣2,求k的值;
(2)试探究k与b的数量关系,并直接写出直线OD的解析式.
【答案】(1)k=12;(2)k=3b2.直线OD的解析式为:y=![]() x.
x.
【解析】
试题分析:(1)首先求出直线y=2x﹣2与坐标轴交点的坐标,然后由△AOB≌△ACD得到CD=OB,AO=AC,即可求出D坐标,由点D在双曲线y=![]() ( x>0)的图象上求出k的值;
( x>0)的图象上求出k的值;
(2)首先直线y=2x+b与坐标轴交点的坐标为A(﹣![]() ,0),B(0,b),再根据△AOB≌△ACD得到CD=DB,AO=AC,即可求出D坐标,把D点坐标代入反比例函数解析式求出k和b之间的关系,进而也可以求出直线OD的解析式.
,0),B(0,b),再根据△AOB≌△ACD得到CD=DB,AO=AC,即可求出D坐标,把D点坐标代入反比例函数解析式求出k和b之间的关系,进而也可以求出直线OD的解析式.
解:(1)当b=﹣2时,直线y=2x﹣2与坐标轴交点的坐标为A(1,0),B(0,﹣2).
∵△AOB∽△ACD,
∴CD=2OB,AO=2AC,
∴点D的坐标为(3,4).
∵点D在双曲线y=![]() ( x>0)的图象上,
( x>0)的图象上,
∴k=3×4=12.
(2)直线y=2x+b与坐标轴交点的坐标为A(﹣![]() ,0),B(0,b).
,0),B(0,b).
∵△AOB∽△ACD,
∴CD=2OB,AC=2AO,
∴点D的坐标为(![]() b,2b)
b,2b)
∵点D在双曲线y=![]() ( x>0)的图象上,
( x>0)的图象上,
∴k=(![]() )(2b)=3b2,即k与b的数量关系为:k=3b2.
)(2b)=3b2,即k与b的数量关系为:k=3b2.
直线OD的解析式为:y=![]() x.
x.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O是坐标原点,矩形OABC的位置如图所示,点A,C的坐标分别为(10,0),(0,8).点P是y轴正半轴上的一个动点,将△OAP沿AP翻折得到△O′AP,直线BC与直线O′P交于点E,与直线OA'交于点F.
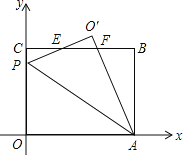
(1)当点P在y轴正半轴,且∠OAP=30°时,求点O′的坐标;
(2)当O′落在直线BC上时,求直线O′A的解析式;
(3)当点P在矩形OABC边OC的运动过程中,是否存在某一时刻,使得线段CF与线段OP的长度相等?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
类别 | 时间t(小时) | 人数 |
A | t≤0.5 | 5 |
B | 0.5<t≤1 | 20 |
C | 1<t≤1.5 | a |
D | 1.5<t≤2 | 30 |
E | t>2 | 10 |
(1)a= ;
(2)补全条形统计图;
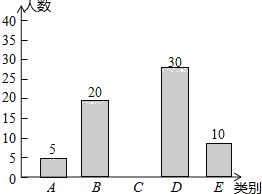
(3)据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住市文化艺术节的商机,某商店决定购进A,B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,
B种纪念品6件,需要800元.
(1)求购进A,B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com