
����Ŀ����ƽ��ֱ������ϵ�У�O������ԭ�㣬����OABC��λ����ͼ��ʾ����A��C������ֱ�Ϊ��10��0������0��8������P��y���������ϵ�һ�����㣬����OAP��AP���۵õ���O��AP��ֱ��BC��ֱ��O��P���ڵ�E����ֱ��OA'���ڵ�F��
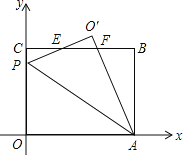
��1������P��y�������ᣬ����OAP=30��ʱ�����O������ꣻ
��2����O������ֱ��BC��ʱ����ֱ��O��A�Ľ���ʽ��
��3������P�ھ���OABC��OC���˶������У��Ƿ����ijһʱ�̣�ʹ���߶�CF���߶�OP�ij�����ȣ������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1����O�������Ϊ��5��5![]() ������2��ֱ��O��A�Ľ���ʽΪy=
������2��ֱ��O��A�Ľ���ʽΪy=![]() x��
x��![]() ����3������P�ھ���OABC��OC���˶������У�����ijһʱ�̣�ʹ���߶�CF���߶�OP�ij�����ȣ���P������Ϊ��0��
����3������P�ھ���OABC��OC���˶������У�����ijһʱ�̣�ʹ���߶�CF���߶�OP�ij�����ȣ���P������Ϊ��0��![]() ����0��
����0��![]() ����
����
��������
�����������1������O��O����O��G��OA�ڵ�G������AO=AO�䣬��O��AO=2��OPA=60�㣬���ɵó���O��AO�ǵȱ������Σ��ٽ�ϵ�A�����꼴�ɵó���O������ꣻ
��2����ֱ��O��A�Ľ���ʽΪy=kx+b�����ݹ��ɶ����ɵó�BO��ij��ȣ��ٸ���O�����߶�BC�Ϻ�O����CB�ӳ����Ϸ�����������ǣ��ɴ˼��ɵó���O������꣬��ϵ�AO����������ô���ϵ�������ɵó�ֱ��O��A�Ľ���ʽ��
��3��������ڣ����P��0��m�������ݵ�O����ֱ��BC�������������������ۣ�����ƽ���ߵ������ҳ���ȵĽǴӶ��ó������������ƣ��ٸ������������ε����ʣ���Ƚǵ����Ǻ���ֵ��ȣ��ҳ������֮��Ĺ�ϵ���ɴ˼����г�����m�ķ��̣��ⷽ�̼��ɵó����ۣ�
�⣺��1������O��O����O��G��OA�ڵ�G����ͼ1��ʾ��
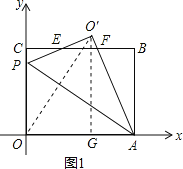
��O��AO=2��OPA=60�㣬AO=AO�䣬
���O��AO�ǵȱ������Σ�
����A��������10��0����
��OA=10��OG=![]() OA=5��O��G=
OA=5��O��G=![]() OA=5
OA=5![]() ��
��
����O���������5��5![]() ����
����
��2����ֱ��O��A�Ľ���ʽΪy=kx+b��
��Rt��ABO����AO��=10��AB=8��
��BO���T6��
�ٵ�O�����߶�BC��ʱ��CO��=10��6=4��
����O���������4��8����
����![]() ����ã�
����ã�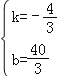 ��
��
����ʱֱ��O��A�Ľ���ʽΪy=��![]() x+
x+![]() ��
��
�ڵ�O����CB�ӳ�����ʱ��CO��=10+6=16��
����O���������16��8����
����![]() ����ã�
����ã�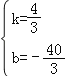
����ʱֱ��O��A�Ľ���ʽΪy=![]() x��
x��![]() ��
��
��3��������ڣ��ɵ�O���λ�ò�ͬ�����������
�ٵ���O����BC���Ϸ�ʱ�����P��0��m��������O����O��G��OA�ڵ�G������P��PQ��O��G�ڵ�Q����ͼ2��ʾ��

��OP=CF��
��BF=BC��CF=10��m��
����C��0��8����
��AB=OC=8��
��Rt��ABF��AB=8��BF=10��m��
��AF=![]() =
=![]() ��
��
��O��G��x�ᣬAB��OA��
��O��G��AB��
���O��GA�ס�ABF��
��![]() ��
��
��O��G=![]() ��AG=
��AG=![]() ��
��
��O��Q=O��G��OP=![]() ��m��PQ=OA��AG=10��
��m��PQ=OA��AG=10��![]() ��
��
�ߡ�PO��Q+��O��PQ=90�㣬��PO��Q+��AO��G=90�㣬
���O��PQ=��AO��G=��FAB��
��![]() ��
��
��PQ=![]() =10��
=10��![]() ��
��
��ã�m1=![]() ��m2=10��
��m2=10��
������m1=![]() �Ƿ�ʽ���̵Ľ⣬
�Ƿ�ʽ���̵Ľ⣬
��ʱ��P������Ϊ��0��![]() ����
����
�ڵ���O����BC���·�ʱ����AF��y��Ľ���ΪM����ͼ3��ʾ��

���P��0��m������CF=OP=m��
BF=10+m��AB=8��OA=10��AF=![]() =
=![]() ��
��
��BC��AO��
���AFB=��MAO��
��![]() ��
��
��OM=![]() ��
��
��PM=OM��OP=![]() ��m��
��m��
�ߡ�MPO������AMO���࣬
���MPO��=��AFB��
��![]() ����
����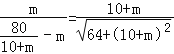 ��
��
��ã�m3=![]() ��m4=��10����ȥ����
��m4=��10����ȥ����
������m3=![]() �Ƿ�ʽ���̵Ľ⣬
�Ƿ�ʽ���̵Ľ⣬
��ʱ��P������Ϊ��0��![]() ����
����
���Ͽ�֪������P�ھ���OABC��OC���˶������У�����ijһʱ�̣�ʹ���߶�CF���߶�OP�ij�����ȣ���P������Ϊ��0��![]() ����0��
����0��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=��x+b�뷴��������![]() ��ͼ���ཻ�ڵ�A��a��3��������x���ཻ�ڵ�B��
��ͼ���ཻ�ڵ�A��a��3��������x���ཻ�ڵ�B��
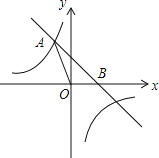
��1����a��b��ֵ��
��2������P��x���ϣ�����AOP���������AOB�������![]() �����P�����꣮
�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����е�ʽһ���������ǣ� ��
A.2a2��3a2=��a2
B.��a+2��2=a2+4
C.a6��a3=a2
D.��a+3����a��3��=a2��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����M=��x��3����x��7����N=��x��2����x��8������M��N�Ĺ�ϵΪ�� ��
A.M��N
B.M��N
C.M=N
D.����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��6��1����6��7��ÿ����ߡ�������µ�����ͳ��ͼ��
�����������ͳ��ͼ���ش��������⣺
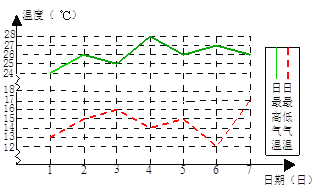
��1������7���У����²�����һ����6��_____�գ�
��2������7�����������µ�ƽ������
��3������7����������µķ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P�ڵ��������ڣ�P��x��ľ�����4����y��ľ�����3����ô��P������Ϊ�� ��
A. ��-4,3�� B. ��-3,4�� C. ��4��-3�� D. ��3��-4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꼶1������ίԱС��ȥΪ�༶�������ֵ��۷ֱ�Ϊ8Ԫ��10Ԫ�����ԣ�����100Ԫ����С����100Ԫǡ�����꣬���м��ֹ����� ��
A. 2 B. 3 C. 4 D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=2x+b��b��0���������ύ��A��B���㣬��˫����y=![]() ��x��0������D�㣬����D��DC��x�ᣬ����ΪC������OD����֪��AOB�ס�ACD�����Ʊ�Ϊ
��x��0������D�㣬����D��DC��x�ᣬ����ΪC������OD����֪��AOB�ס�ACD�����Ʊ�Ϊ![]() ��
��
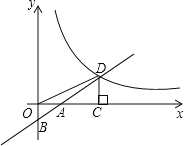
��1�����b=��2����k��ֵ��
��2����̽��k��b��������ϵ����ֱ��д��ֱ��OD�Ľ���ʽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com