
����Ŀ����ͼ��ֱ��y=![]()
![]() x+8��x�ύ��A�㣬��y�ύ�ڵ�B������P��A���������ÿ��2����λ�ٶ�������AO�����˶���ͬʱ����Q��B���������ÿ��1����λ���ٶ�������BA�������A�����˶�����һ����ֹͣ�˶�����һ����Ҳ��ֹ֮ͣ�˶�������PQ�����˶���ʱ��Ϊt���룩��
x+8��x�ύ��A�㣬��y�ύ�ڵ�B������P��A���������ÿ��2����λ�ٶ�������AO�����˶���ͬʱ����Q��B���������ÿ��1����λ���ٶ�������BA�������A�����˶�����һ����ֹͣ�˶�����һ����Ҳ��ֹ֮ͣ�˶�������PQ�����˶���ʱ��Ϊt���룩��
��1����t�Ĵ���ʽ��ʾAP= ��AQ=
��2����tΪ��ֵʱ��PQ��OB��
��3������CΪƽ��ֱ������ϵ��һ�㣬�Ƿ����tֵ��ʹ����A��P��Q��CΪ������ı���Ϊ���Σ������ڣ����Q�����꣬�������ڣ���˵�����ɣ�

���𰸡���1��![]() ��
��![]() ����2��
����2��![]() ����3����
����3����![]() ������Ϊ
������Ϊ![]() ��
��![]() ��
��![]() ��
��
��������
��1���������⣬�������A�͵�B�����꣬�õ�AB�ij��ȣ�����·��=�ٶ�![]() ʱ�䣬���ɱ�ʾ��AP��BQ��
ʱ�䣬���ɱ�ʾ��AP��BQ��
��2���ɣ�1����֪AP��AQ��Ȼ������ƽ���߷��߶γɱ������������t��ֵ��
��3�������������г�������⣺�ٵ�![]() ����
����![]() ��
��![]() ���ɵ�����
���ɵ�����![]() ���ڵ�
���ڵ�![]() ʱ����
ʱ����![]() ��
��![]() ���ɵ�����
���ɵ�����![]() ���۵�
���۵�![]() ʱ����
ʱ����![]() ��
��![]() ���ɵ�����
���ɵ�����![]() ���ֱ������Q�����꼴��.
���ֱ������Q�����꼴��.
�⣺��1���������⣬��![]() ����
����![]() �����
�����![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��![]() ��
��
���![]() ��
��![]() ��
��
��![]() �У��ɹ��ɶ����ã�
�У��ɹ��ɶ����ã�![]() ��
��
�ߵ�![]() ���ٶ���ÿ��2����λ����
���ٶ���ÿ��2����λ����![]() ���ٶ���ÿ��1����λ��
���ٶ���ÿ��1����λ��
��![]() ��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ��
��
��2����![]() ����ͼ��
����ͼ��
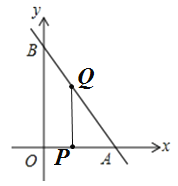
��![]() ��
��
��![]() ��
��
��![]() ����ã�
����ã�![]() ��
��
��3������ͼ�У���![]() ����
����![]() ��
��![]() ���ɵ�����
���ɵ�����![]() ��
��
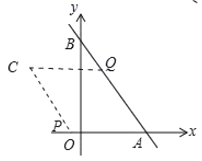
��![]() ��
��
��![]() ��
��
��![]() ��
��
���Q��![]() ��
��![]() ����
����
��![]() ��
��
��ã�![]() ��
��
��![]() ��
��
���ʱ![]() ��
��
����ͼ�У���![]() ʱ����
ʱ����![]() ��
��![]() ���ɵ�����
���ɵ�����![]() ������
������![]() ��
��![]() ��
��![]() ��
��
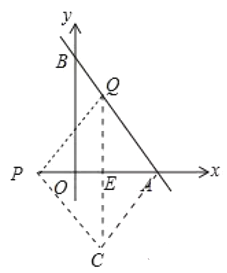
���ı���![]() �����Σ�
������
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
���ͬ�������Q�����꣬
���ʱ![]() ��
��
����ͼ�У���![]() ʱ����
ʱ����![]() ��
��![]() ���ɵ�����
���ɵ�����![]() ������
������![]() ��
��![]() ��
��![]() ��
��
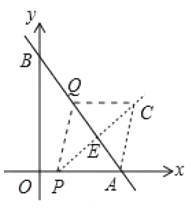
���ı���![]() �����Σ�
������
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��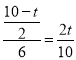 ��
��
��![]() ��
��
���ͬ�������Q�����꣬
���ʱ![]() ��
��
�������������������ĵ�![]() ������Ϊ��
��������![]() ��
��![]() ��
��![]() ��
��


 ��У���˿��ֿ���ϵ�д�
��У���˿��ֿ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�ֱ��y4x4��x�ᣬy��ֱ��ڵ�A��B����A��������yax2bx3a��a0���ϣ�����B����ƽ��3����λ���ȣ��õ���C��
��1�������ߵĶ�������Ϊ ���ú�a�Ĵ���ʽ��ʾ��
��2����a1����t��1��x��tʱ������yax2bx3a��a0�������ֵΪy1����СֵΪy2����y1y22����t��ֵ��
��3�������������߶�BCǡ��һ�������㣬��Ϻ���ͼ����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
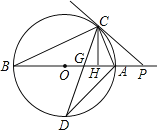
����Ŀ����ͼ��AB����O��ֱ����PΪBA�ӳ�����һ�㣬��P����O�����ߣ��е�ΪC��CDƽ�֡�ACB����O��D����AB��G��
��1����֤����PAC�ס�PCB��
��2����֪��O�İ뾶Ϊ5��PC��2![]() ����C��CH��AB��H��
����C��CH��AB��H��
����tan��ADC��
����GH�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A�������ǣ�4��0��������OA=OC=4OB������P�ڹ�A��B��C������������ϣ�
��1���������ߵĽ���ʽ��
��2����AC�Ϸ�������������һ����G����ͼ������G�˶���ijλ��ʱ����AG��AOΪ�ڱߵ�ƽ���ı��ε��ĸ�����ǡ��Ҳ���������ϣ������ʱ��G�����ꣻ
��3�����������ϴ��ڵ�P��ʹ�á�ACP����ACΪֱ�DZߵ�ֱ�������Σ�ֱ��д�����з��������ĵ�P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
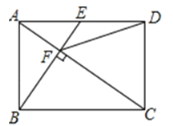
����Ŀ���ھ���ABCD�У���EΪAD���е㣬����BE��AC��AC��BE�ڵ�F������DF�����ڽ��ۢ�CF=2AF�ڡ�AEF�ס�CAB��DF=DC��tan��CAD=![]() ��ȷ����_______________��
��ȷ����_______________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǡ�O���ڽ������Σ�AB�ǡ�O��ֱ����OF��AB����AC�ڵ�F����E��AB���ӳ����ϣ�����EM������C���ҡ�ACE+��AFO=180��.
��1����֤��EM�ǡ�O�����ߣ�
��2������A=��E,BC=![]() ������Ӱ���ֵ����.���������
������Ӱ���ֵ����.���������![]() ���ţ�.
���ţ�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��עѧ�����а�ȫ��������ij��ѧ�����з�ʽ����������Ϊ���ࣺA�������г���B�����У�C����������ʿ��D���������������˽�����Ƴ�����������������ͳ��ͼ��
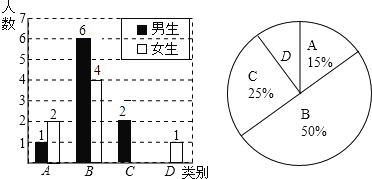
�������ͳ��ͼ������������⣺
��1������һ�������˶�����ѧ����
��2��C��Ů������ ������D���������� ��������������ͳ��ͼ����������
��3�����ӱ������A���D��ѧ�����ֱ����ѡȡһλͬѧ���н�һ�����飬�����б�������״ͼ�ķ��������ѡͬѧ��ǡ����һλ��ͬѧ��һλŮͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����6�֣���ͼ����ABC�������������ֱ�ΪA��2��4����B��1��1����C��4��3����

��1���뻭����ABC����x��ԳƵ���A1B1C1����д����A1�����ꣻ
��2���뻭����ABC�Ƶ�B��ʱ����ת90�������A2BC2��
��3�������2����C����ת��C2����������·�������ǹ��������ź�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ȵ��������εĶ��壬���Ƕ��壺��һ���ڱ���ȵ��ı��ν��������ڱ��ı�������
��1����������
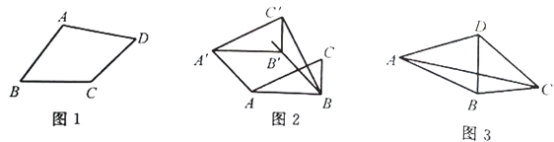
��ͼ1�����ı���ABCD�У�����һ������ʹ���ı���ABCD�������ڱ��ı���������д�������ӵ�һ��������
��2������̽��
��С����룺�Խ�����ƽ�ֵ������ڱ��ı����������Σ����IJ�����ȷ����˵�����ɣ�
����ͼ2��С�컭��һ��Rt��ABC��������ABC=90����AB=2��BC=1������Rt��ABC����ABC��ƽ����BB������ƽ�Ƶõ���A��B��C��������AA����BC����С��Ҫ��ƽ�ƺ���ı���ABC��A���������ڱ��ı�������Ӧƽ�ƶ��پ��루���߶�BB���ij�����
��3��Ӧ����չ
��ͼ3�������ڱ��ı�����ABCD�У�AB=AD����BAD+��BCD==90����AC��BDΪ�Խ��ߣ�AC=![]() AB����̽��BC��CD��BD��������ϵ��
AB����̽��BC��CD��BD��������ϵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com