
����Ŀ����ƽ��ֱ������ϵxOy�У�ֱ��y4x4��x�ᣬy��ֱ��ڵ�A��B����A��������yax2bx3a��a0���ϣ�����B����ƽ��3����λ���ȣ��õ���C��
��1�������ߵĶ�������Ϊ ���ú�a�Ĵ���ʽ��ʾ��
��2����a1����t��1��x��tʱ������yax2bx3a��a0�������ֵΪy1����СֵΪy2����y1y22����t��ֵ��
��3�������������߶�BCǡ��һ�������㣬��Ϻ���ͼ����a��ȡֵ��Χ��
���𰸡���1��![]() ����2��
����2��![]() ��
��![]() ����3��
����3��![]() ��
��![]() ʱ�����������߶�
ʱ�����������߶�![]() ��һ�����㣮
��һ�����㣮
��������
��1����A��-1��0�����������ߵ�b=-2a���ٽ������߽���ʽ��Ϊ����ʽ������⣻
��2����a=-1ʱ�������߶�������Ϊ��1��4����Ȼ���������������ߵ����ʼ��ɽ��
��3�������B���꣬����B����ƽ��3����λ���ȣ��õ���C�����������ߵĶ���������⣮
�⣺��1��ֱ��y=4x+4��x�ᣬy��ֱ��ڵ�A��B��
��A��-1��0����B��0��4����
��A��������y=ax2+bx-3a��a��0���ϣ�
��b=-2a��
��������y=ax2+bx-3a=a��x-1��2-4a��
�������ߵĶ�������Ϊ��1��-4a����
�ʴ�Ϊ��![]() ��
��
��2����![]() ��
��
�������ߵĽ���ʽΪ![]() ��
��
�ٵ�![]() ʱ��
ʱ��
![]() ��
��
��![]() ��
��
�ڵ�![]() ʱ����
ʱ����![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��
�۵�![]() ʱ��
ʱ��![]() ��
��
��ã�![]() ����ȥ����
����ȥ����
�ܵ�![]() ʱ��
ʱ��![]() ��
��
��ã�![]() ����ȥ����
����ȥ����
��![]() ��
��![]() ��
��
��3���ٰ�![]() ���������ߣ���
���������ߣ���![]() ��
��
�����������߶�![]() ֻ��һ�������㣬
ֻ��һ�������㣬
��![]() ��
��
��![]() ��
��
�ڵ������߶������߶�![]() ��ʱ��������Ϊ
��ʱ��������Ϊ![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ʱ�����������߶�
ʱ�����������߶�![]() ��һ�����㣮
��һ�����㣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ֣���������ѧΪ�˽�ѧ�������Ķ�����ʱ���������Ӹ��꼶ѧ������������һ����ѧ������ͳ�ƣ���������Դ˴�ͳ���������IJ�������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ�������ͼ����Ϣ�ش��������⣺
��� | ʱ��Σ�Сʱ�� | Ƶ�� | Ƶ�� |
1 | 0��x��0.5 | 10 | 0.05 |
2 | 0.5��x��1.0 | 20 | 0.10 |
3 | 1.0��x��1.5 | 80 | b |
4 | 1.5��x��2.0 | a | 0.35 |
5 | 2.0��x��2.5 | 12 | 0.06 |
6 | 2.5��x��3.0 | 8 | 0.04 |
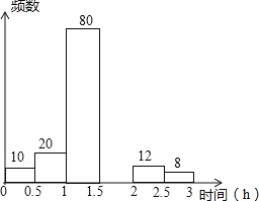
��1������a=______b=______��
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3�������У�ѧ�����Ķ�����ʱ�����λ�����ڵ�______�飻
��4����У����ѧ��3000�ˣ������ѧ�����Ķ���������1.5Сʱ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪:�ھ���![]() �У�
��![]() ��
��![]() �ֱ��DZ�
�ֱ��DZ�![]() ��
��![]() �ϵĵ㣬����
�ϵĵ㣬����![]() ��
��![]() �Ĵ��߽�
�Ĵ��߽�![]() �ڵ�
�ڵ�![]() ����
����![]() Ϊֱ������Բ
Ϊֱ������Բ![]() ��
��
��1����գ���![]() _____________����������������������
_____________����������������������![]() �ϣ���
�ϣ���![]() ʱ��
ʱ��![]() ��ֵ��_____________��
��ֵ��_____________��
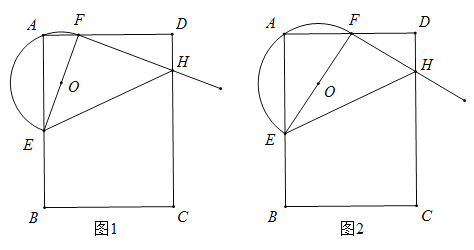
��2����ͼ1����![]() �У���
�У���![]() ʱ����֤��
ʱ����֤��![]() ��
��
��3����ͼ2����![]() �Ķ���
�Ķ���![]() �DZ�
�DZ�![]() ���е�ʱ����ֱ��д��
���е�ʱ����ֱ��д��![]() �����߶ε�������ϵ��
�����߶ε�������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ҷ�ǰ���ʡ��Ҫ��������֮һ��2020���²������ڼ䣬ij�賧Ϊ���������棬�����г����飬���²�۸�Ϊ400Ԫ/kg����������������������������x�죨1��x��15����xΪ�������Ʋ�ɱ�������ժ�ͼӹ������Ʋ����������Ϣ���±����ٶ��ò賧ÿ�����������۵��²�û����ʧ�������ڵ���ȫ���۳�����������=�����۶�-���Ʋ�ɱ���
�Ʋ�ɱ���Ԫ/kg�� | 150+10x |
�Ʋ�����kg�� | 40+4x |
��1������ò賧��10������룻
��2����ò賧��x�������Ϊy��Ԫ���������y��x֮��ĺ�����ϵʽ�������y�����ֵ����ʱx��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ3cm��EΪCD����һ�㣬��DAE=30����MΪAE���е㣬����M��ֱ�߷ֱ���AD��BC�ཻ�ڵ�P��Q����PQ=AE����AP���� cm��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
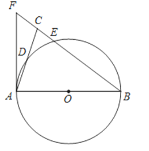
����Ŀ����ͼ������ABC�У�BA=BC����ABΪֱ���ġ�O�ֱ�AC��BC�ڵ�D��E��BC���ӳ������O������AF���ڵ�F��
��1����֤����ABC=2��CAF��
��2����AC=2![]() ��CE��EB=1��4����CE��AF�ij���
��CE��EB=1��4����CE��AF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���![]() �У�
��![]() ����
����![]() ��
��![]() ���ϵ�һ�����㣬���ı���
���ϵ�һ�����㣬���ı���![]() ��ֱ��
��ֱ��![]() �۵����õ��ı���
�۵����õ��ı���![]() ����
����![]() ��
��![]() �Ķ�Ӧ��ֱ�Ϊ��
�Ķ�Ӧ��ֱ�Ϊ��![]() ��
��![]() ��ֱ��
��ֱ��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
��1����֤��![]() ��
��
��2������![]() ����֪
����֪![]() ��
��
����ͼ������![]() ��
��![]() ʱ����
ʱ����![]() �ij��ȣ�
�ij��ȣ�
����ͼ�������ı���![]() Ϊ����ʱ����ֱ��д��
Ϊ����ʱ����ֱ��д��![]() �ij��ȣ�
�ij��ȣ�
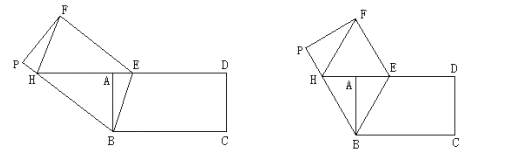
ͼ�� ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��һ���á������������㣬��������ʵ��a��b������a��b��b2+2a+1������7��4��42+2��7+1��31��
��1����֪��m��3�Ľ���ǩ�4����m���� ����
��2��������ʵ��2n��n��2�������¶��塰��������㣬���Ϊ9����n��ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ���������Ա���xȡaʱ������ֵyҲ����a�����dz�aΪ��������IJ�����.������κ���y��x2+2x+c����������IJ�����x1��x2����x1��1��x2����c��ȡֵ��Χ��( )
A. c����3B. c����2C. c��![]() D. c��1
D. c��1
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com