
【题目】 郑州外国语中学为了解学生课下阅读所用时间的情况,从各年级学生中随机抽查了一部分学生进行统计,下面是针对此次统计所制作的不完整的频数分布表和频数分布直方图,请根据图表信息回答下列问题:
组别 | 时间段(小时) | 频数 | 频率 |
1 | 0≤x<0.5 | 10 | 0.05 |
2 | 0.5≤x<1.0 | 20 | 0.10 |
3 | 1.0≤x<1.5 | 80 | b |
4 | 1.5≤x<2.0 | a | 0.35 |
5 | 2.0≤x<2.5 | 12 | 0.06 |
6 | 2.5≤x<3.0 | 8 | 0.04 |
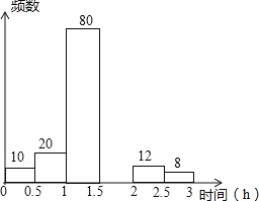
(1)表中a=______b=______;
(2)请补全频数分布直方图;
(3)样本中,学生日阅读所用时间的中位数落在第______组;
(4)该校共有学生3000人,请估计学生日阅读量不少于1.5小时的人数.
【答案】(1)70,0.40;(2)详见解析;(3)3;(4)1350
【解析】
(1)根据“频数÷百分比=数据总数”先计算总数为200人,再根据表中的数分别求a和b;
(2)根据a的值即可补全频数直方图;
(3)第100和第101个学生读书时间都在第3组;
(4)后三组的读书时间不少于1.5小时,用总数3000乘以这三组的百分比之和即可.
解:(1)∵调查的总人数为10÷0.05=200,
∴a=200×0.35=70,b=80÷200=0.40,
故答案为:70,0.40;
(2)补全直方图,如下图:
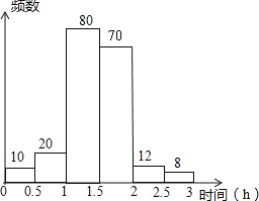
(3)样本中一共有200人,中位数是第100和101人的读书时间的平均数,
即第3组:1~1.5小时;
故答案为:3;
(4)3000×(0.35+0.06+0.04)=1350(人),
答:估计该校学生日阅读量不少于1.5小时的人数为1350.


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:初中数学 来源: 题型:
【题目】某校在宣传“民族团结”活动中,采用四种宣传形式:A.器乐,B.舞蹈,C.朗诵,D.唱歌.每名学生从中选择并且只能选择一种最喜欢的,学校就宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图.

请结合图中所给信息,解答下列问题:
(1)本次调查的学生共有_____人;
(2)补全条形统计图;
(3)该校共有1200名学生,请估计选择“唱歌”的学生有多少人?
(4)七年一班在最喜欢“器乐”的学生中,有甲、乙、丙、丁四位同学表现优秀,现从这四位同学中随机选出两名同学参加学校的器乐队,请用列表或画树状图法求被选取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
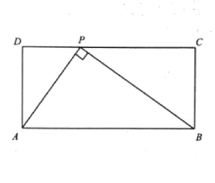
【题目】如图1,在矩形![]() 的边
的边![]() 上存在点
上存在点![]() ,使得
,使得![]() ,我们称点
,我们称点![]() 为矩形的“和谐点
为矩形的“和谐点
(1)求证: ![]() ;
;
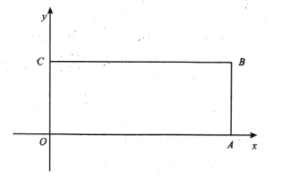
(2)如图2,矩形![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() 为坐标原点,点
为坐标原点,点![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,在
轴上,在![]() 边上是否存在“和谐点”
边上是否存在“和谐点”![]() ,如果存在,求出点
,如果存在,求出点![]() 的坐标;如果不存在,请说明理由
的坐标;如果不存在,请说明理由
(3)在(2)中,如果点![]() 的坐标为
的坐标为![]() ,且在
,且在![]() 上存在“和谐点”
上存在“和谐点”![]() 求
求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年春节,一场突如其来的新型冠状肺炎病毒疫情在武汉突发,为响应党中央号召,在“支援武汉,防控疫情”的过程中,某省计划组织1441名医护人员的“援汉”团队前往武汉进行支援,经过研究,决定租用当地租车公司一共62辆![]() 、
、![]() 两种型号客车作为交通工具,下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
两种型号客车作为交通工具,下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号 | 载客量 | 租金单价 |
| 30人 | 380元 |
| 20人 | 280元 |
注:载客量指的是每辆客车最多可载医护人员的人数.
(1)设租用![]() 型号客车
型号客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元,求
元,求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若要使租车总费用不超过19900元,一共有几种租车方案?哪种租车方案最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设点A(x1,y1)和点B(x2,y2)是反比例函数y=![]() 图象上的两点,当x1<x2<0时,y1>y2,则一次函数y=-2x+k的图象不经过的象限是( )
图象上的两点,当x1<x2<0时,y1>y2,则一次函数y=-2x+k的图象不经过的象限是( )
A.第一象限B.第二象限C.第三象限D.第四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,在
,在![]() 轴上有一动点
轴上有一动点![]() ,过点
,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
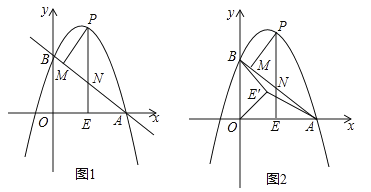
(1)求![]() 的值和直线
的值和直线![]() 的函数表达式;
的函数表达式;
(2)设![]() 的周长为
的周长为![]() ,
,![]() 的周长为
的周长为![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
(3)如图2,在(2)条件下,将线段![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,旋转角为
,旋转角为![]() ,连接
,连接![]() 、
、![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两条抛物线![]() 与
与![]() 的顶点相同.
的顶点相同.
(1)求抛物线![]() 的解析式;
的解析式;
(2)点![]() 是抛物找
是抛物找![]() 在第四象限内图象上的一动点,过点
在第四象限内图象上的一动点,过点![]() 作
作![]() 轴,
轴,![]() 为垂足,求
为垂足,求![]() 的最大值;
的最大值;
(3)设抛物线![]() 的顶点为点
的顶点为点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,问在
,问在![]() 的对称轴上是否存在点
的对称轴上是否存在点![]() ,使线段
,使线段![]() 绕点
绕点![]() 顺时针旋转90°得到线段
顺时针旋转90°得到线段![]() ,且点
,且点![]() 恰好落在抛物线
恰好落在抛物线![]() 上?若存在,求出点
上?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y4x4与x轴,y轴分别交于点A,B,点A在抛物线yax2bx3a(a0)上,将点B向右平移3个单位长度,得到点C.
(1)抛物线的顶点坐标为 (用含a的代数式表示)
(2)若a1,当t-1≤x≤t时,函数yax2bx3a(a0)的最大值为y1,最小值为y2,且y1y22,求t的值;
(3)若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com