
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 分别与
分别与![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
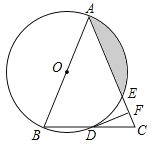
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() 的半径为
的半径为![]() ,
,![]() ,求阴影部分的面积.
,求阴影部分的面积.
【答案】(1)见解析;(2)S阴影=![]() .
.
【解析】
(1)连接OD,先说明OD∥AC,再得到OD⊥DF,即可完成证明;
(2)连接OE,过O作OM⊥AC于M,先求出AE、OM的长和∠AOE的度数,再分别求出S△AOE和S扇形AOE,最后根据S△AOE-S扇形AOE解答即可;
(1)证明:连接OD,
∵OB=OD
∴∠ABC=∠ODB
∵AB=AC
∴∠ABC=∠ACB
∴∠ODB=∠ACB
∴OD∥AC
∵![]()
∴OD⊥DF
∴DF是⊙O的切线
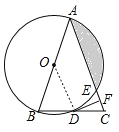
(2)解:连接OE,过O作OM⊥AC于M
∵DF⊥AC,∠CDF=15°
∴∠ABC=∠ACB=75°
∴∠BAC=30°.
∵OA=OE
∴∠AOE=120°
∵⊙O的半径为3
∴S扇形AOE=![]() =
=![]()
∵∠BAC=30°
∵OA=OE=3
∴![]()
∵OM⊥AC,
∴ AE=2AM=![]() ,
,
∴S△AOE=![]()
∴S阴影=![]() .
.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于A,B两点,与y轴交于点C(0,﹣2),点A的坐标是(2,0),P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E,抛物线的对称轴是直线x=﹣1.
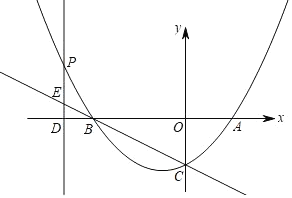
(1)求抛物线的函数表达式;
(2)若点P在第二象限内,且PE=![]() OD,求△PBE的面积.
OD,求△PBE的面积.
(3)在(2)的条件下,若M为直线BC上一点,在x轴的上方,是否存在点M,使△BDM是以BD为腰的等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛.为了了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根据调査结果绘制成的统计图(部分)如图

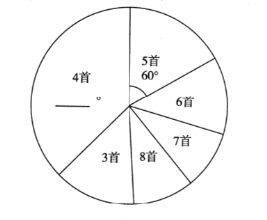
大赛结束后一个月,再次抽查这部分学生的周诗词诵背数量,绘制成如下统计表:
诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 10 | 10 | 15 | 40 | 25 | 20 |
请根据调查的信息分析
(1)学校团委一共抽取了多少名学生进行调查
(2)大赛前诵背4首人数所在扇形的圆心角为 ,并补充完条形统计图
(3)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是![]() 的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且
的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且![]() ,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.
,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.

(1)求证:BD是⊙O的切线;(2)当OB=2时,求BH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
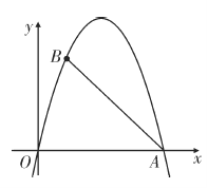
【题目】如图,抛物线![]() 过坐标原点和
过坐标原点和![]() ,
,![]() 两点.
两点.
(1)求该抛物线的表达式;
(2)在线段![]() 右侧的抛物线上是否存在一点
右侧的抛物线上是否存在一点![]() ,使得
,使得![]() 分
分![]() 的面积为
的面积为![]() 两部分?若存在,求出点
两部分?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 郑州外国语中学为了解学生课下阅读所用时间的情况,从各年级学生中随机抽查了一部分学生进行统计,下面是针对此次统计所制作的不完整的频数分布表和频数分布直方图,请根据图表信息回答下列问题:
组别 | 时间段(小时) | 频数 | 频率 |
1 | 0≤x<0.5 | 10 | 0.05 |
2 | 0.5≤x<1.0 | 20 | 0.10 |
3 | 1.0≤x<1.5 | 80 | b |
4 | 1.5≤x<2.0 | a | 0.35 |
5 | 2.0≤x<2.5 | 12 | 0.06 |
6 | 2.5≤x<3.0 | 8 | 0.04 |
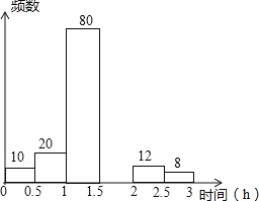
(1)表中a=______b=______;
(2)请补全频数分布直方图;
(3)样本中,学生日阅读所用时间的中位数落在第______组;
(4)该校共有学生3000人,请估计学生日阅读量不少于1.5小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
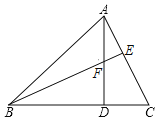
【题目】已知锐角△ABC,∠ABC=45°,AD⊥BC于D,BE⊥AC于E,交AD于F.
(1)求证:△BDF≌△ADC;
(2)若BD=4,DC=3,求线段BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究.
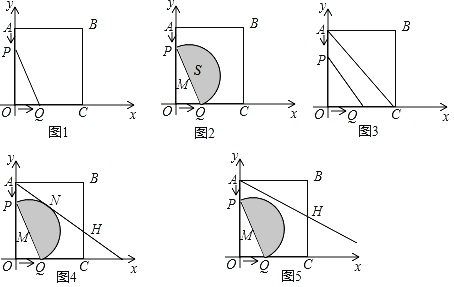
如图,在平面直角坐标系中,A(0,8),C(6,0),以O,A,C为顶点作矩形OABC,动点P从点A出发,沿AO以4个单位每秒的速度向O运动;同时动点Q从点O出发沿OC以3个单位每秒的速度向C运动.设运动时间为t,当动点P,Q中的任何一个点到达终点后,两点同时停止运动.连接PQ.
(情景导入)当t=1时,求出直线PQ的解析式.
(深入探究)①连接AC,若△POQ与△AOC相似,求出t的值.
②如图,取PQ的中点M,以QM为半径向右侧作半圆M,直接写出半圆M的面积的最小值,并直接写出此时t的值.
(拓展延伸)如图,过点A作半圆M的切线,交直线BC于点H,于半圆M切于点N.
①在P,Q的整个运动过程中,点H的运动路径为 .
②若固定点H(6,2)不动,则在整个运动过程中,半圆M能否与梯形AOCH相切?若能,求出此时t的值;若不能,请证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于 cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com