
【题目】如图,抛物线![]() 过坐标原点和
过坐标原点和![]() ,
,![]() 两点.
两点.
(1)求该抛物线的表达式;
(2)在线段![]() 右侧的抛物线上是否存在一点
右侧的抛物线上是否存在一点![]() ,使得
,使得![]() 分
分![]() 的面积为
的面积为![]() 两部分?若存在,求出点
两部分?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
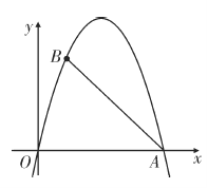
【答案】(1)![]() ;(2)存在,点
;(2)存在,点![]() 的坐标为
的坐标为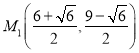 ,
,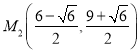 .
.
【解析】
(1)将点![]() 、A、B的坐标代入抛物线表达式,即可求解;
、A、B的坐标代入抛物线表达式,即可求解;
(2)先求AB直线的解析式,再证明![]() ,设点
,设点![]() 坐标为
坐标为![]() ,表示出Q点坐标,分①当
,表示出Q点坐标,分①当![]() 时,②当
时,②当![]() 时,求出M的坐标.
时,求出M的坐标.
解:(1)将点![]() ,
,![]() ,
,![]() 的坐标代入抛物线表达式得,
的坐标代入抛物线表达式得,
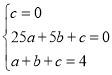 ,
,
解得: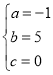 ,
,
![]() 抛物线的表达式为:
抛物线的表达式为:![]() ;
;
(2)存在,理由如下:
设直线![]() 的表达式为:
的表达式为:![]() ,
,
![]() ,
,![]() ,
,
![]() ,解得:
,解得:![]() .
.
![]() 直线
直线![]() 的表达式为:
的表达式为:![]() ,
,
令![]() ,则
,则![]() ,
,
![]() 直线
直线![]() 交
交![]() 轴于点
轴于点![]() ,如图
,如图
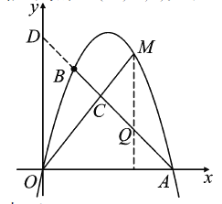
设![]() 交
交![]() 于点
于点![]() ,
,
当![]() 或
或![]() 时,
时,![]() 分
分![]() 的面积为
的面积为![]() ,
,
过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
由点![]() 在抛物线上,可设点
在抛物线上,可设点![]() 坐标为
坐标为![]() ,
,
由点![]() 在直线
在直线![]() 上,则点
上,则点![]() 坐标为
坐标为![]() ,
,
①当![]() 时,则有:
时,则有:![]() ,解得:
,解得:![]() ,
,
由![]() ,
,
即![]() ,解得:
,解得:![]() ,
,
即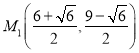 ,
,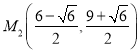 ,
,
②当![]() 时,则有:
时,则有:![]() ,
,
解得:![]() ,
,
由![]() ,
,
所得方程无解,
综上所述,点![]() 的坐标为
的坐标为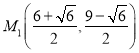 ,
,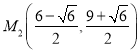 .
.


科目:初中数学 来源: 题型:
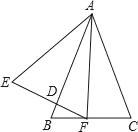
【题目】如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:①∠AFC=∠C;②DF=BF;③△ADE∽△FDB;④∠BFD=∠CAF.其中正确的结论是_____(填写所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
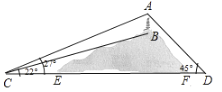
【题目】如图,山顶有一塔![]() ,塔高
,塔高![]() .计划在塔的正下方沿直线
.计划在塔的正下方沿直线![]() 开通穿山隧道
开通穿山隧道![]() .从与
.从与![]() 点相距
点相距![]() 的
的![]() 处测得
处测得![]() 、
、![]() 的仰角分别为
的仰角分别为![]() 、
、![]() ,从与
,从与![]() 点相距
点相距![]() 的
的![]() 处测得
处测得![]() 的仰角为
的仰角为![]() .求隧道
.求隧道![]() 的长度.(参考数据:
的长度.(参考数据:![]() ,
,![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,过点
两点,过点![]() 的直线
的直线![]() 交抛物线于点
交抛物线于点![]() .
.
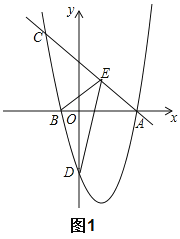
(1)求此抛物线的解析式;
(2)在线段![]() 上有一动点
上有一动点![]() ,当点
,当点![]() 在某个位置时,
在某个位置时,![]() 的面积为
的面积为![]() ,求此时
,求此时![]() 点坐标;
点坐标;
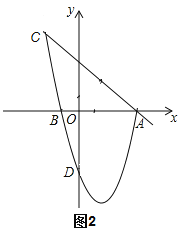
(3)如图2,当动点![]() 在直线
在直线![]() 与抛物线围成的封闭线
与抛物线围成的封闭线![]() 上运动时,是否存在以
上运动时,是否存在以![]() 为直角边的直角三角形
为直角边的直角三角形![]() ,若存在,请求出符合要求的所有
,若存在,请求出符合要求的所有![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 为
为![]() .
.
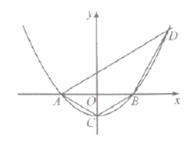
(1)求抛物线的解析式.
(2)过点![]() 作直线
作直线![]() 与抛物线在第一象限的交点为
与抛物线在第一象限的交点为![]() .当
.当![]() 时,确定直线
时,确定直线![]() 与
与![]() 的位置关系.
的位置关系.
(3)在第二象限抛物线上求一点![]() ,使
,使![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情期间,甲、乙两家网店以同样价格销售相同的防疫用品,它们的优惠方案分别为:甲店,一次性购物中超过100元后的价格部分打七折;乙店,一次性购物中超过500元后的价格部分打五折,设商品原价为![]() 元(
元(![]() ),购物应付金额为
),购物应付金额为![]() 元.
元.
(1)求出在甲店购物时![]() 与
与![]() 之间的函数解析式;
之间的函数解析式;
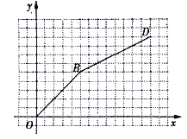
(2)在乙店购物时![]() 与
与![]() 之间的函数图像如图所示(图中线段
之间的函数图像如图所示(图中线段![]() 、射线
、射线![]() ),请在图中画出(l)中所得函数当
),请在图中画出(l)中所得函数当![]() 时的图像,并分别写出该图像与图中
时的图像,并分别写出该图像与图中![]() 、
、![]() 的交点
的交点![]() 和
和![]() 的坐标;
的坐标;
(3)根据函数图像,请直接写出新冠肺炎疫情期间选择哪家网店购物更优惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定一种新的运算△:a△b=a(a+b)﹣a+b.例如,1△2=1×(1+2)﹣1+2=4.
(1)8△9= ;
(2)若x△3=11,求x的值;
(3)求代数式﹣x△4的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2014广州)从广州到某市,可乘坐普通列车或高铁,已知高铁的行驶路程是400千米,普通列车的行驶路程是高铁的行驶路程的1.3倍.
(1)求普通列车的行驶路程;
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需要时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com