
【题目】规定一种新的运算△:a△b=a(a+b)﹣a+b.例如,1△2=1×(1+2)﹣1+2=4.
(1)8△9= ;
(2)若x△3=11,求x的值;
(3)求代数式﹣x△4的最小值.
【答案】(1)137;(2)x1=2,x2=﹣4;(3)![]()
【解析】
(1)根据a△b=a(a+b)﹣a+b,可以求得所求式子的值;
(2)根据a△b=a(a+b)﹣a+b,可以求得所求方程的解;
(3)根据a△b=a(a+b)﹣a+b,可以将题目中的代数式化简,然后利用二次函数的性质,即可得到所求代数式的最小值.
解:(1)∵a△b=a(a+b)﹣a+b,
∴8△9
=8×(8+9)﹣8+9
=8×17﹣8+9
=136﹣8+9
=137,
故答案为:137;
(2)∵x△3=11,
∴x(x+3)﹣x+3=11,
解得,![]() =2,
=2,![]() =﹣4;
=﹣4;
(3)∵﹣x△4
=﹣x(﹣x+4)+x+4
=x2﹣4x+x+4
=![]() ﹣3x+4
﹣3x+4
=![]() +
+![]() ,
,
∴当x=![]() 时,﹣x△4有最小值
时,﹣x△4有最小值![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,以CD为直径的⊙O分别交AC,BC于点E,F两点,过点F作FG⊥AB于点G.

(1)试判断FG与⊙O的位置关系,并说明理由;
(2)若AC=6,CD=5,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
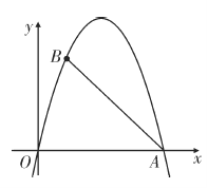
【题目】如图,抛物线![]() 过坐标原点和
过坐标原点和![]() ,
,![]() 两点.
两点.
(1)求该抛物线的表达式;
(2)在线段![]() 右侧的抛物线上是否存在一点
右侧的抛物线上是否存在一点![]() ,使得
,使得![]() 分
分![]() 的面积为
的面积为![]() 两部分?若存在,求出点
两部分?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
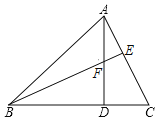
【题目】已知锐角△ABC,∠ABC=45°,AD⊥BC于D,BE⊥AC于E,交AD于F.
(1)求证:△BDF≌△ADC;
(2)若BD=4,DC=3,求线段BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点I为△ABC的内心,AB=4cm,AC=3cm,BC=2cm,将∠ACB平移,使其顶点与点I重合,则图中阴影部分的周长为( )
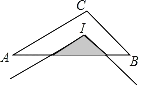
A.1cmB.2cmC.3cmD.4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究.
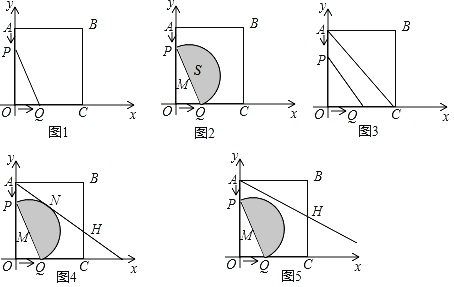
如图,在平面直角坐标系中,A(0,8),C(6,0),以O,A,C为顶点作矩形OABC,动点P从点A出发,沿AO以4个单位每秒的速度向O运动;同时动点Q从点O出发沿OC以3个单位每秒的速度向C运动.设运动时间为t,当动点P,Q中的任何一个点到达终点后,两点同时停止运动.连接PQ.
(情景导入)当t=1时,求出直线PQ的解析式.
(深入探究)①连接AC,若△POQ与△AOC相似,求出t的值.
②如图,取PQ的中点M,以QM为半径向右侧作半圆M,直接写出半圆M的面积的最小值,并直接写出此时t的值.
(拓展延伸)如图,过点A作半圆M的切线,交直线BC于点H,于半圆M切于点N.
①在P,Q的整个运动过程中,点H的运动路径为 .
②若固定点H(6,2)不动,则在整个运动过程中,半圆M能否与梯形AOCH相切?若能,求出此时t的值;若不能,请证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
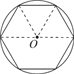
【题目】我国魏晋时期的数学家刘徽创立了“割圆术”,认为圆内接正多边形边数无限增加时,周长就越接近圆周长,由此求得了圆周率π的近似值,设半径为r的圆内接正n边形的周长为L,圆的直径为d,如图所示,当n=6时,π≈![]() =
=![]() =3,那么当n=12时,π≈
=3,那么当n=12时,π≈![]() ≈________(结果精确到0.01,参考数据:sin15°=cos75°≈0.259).
≈________(结果精确到0.01,参考数据:sin15°=cos75°≈0.259).
查看答案和解析>>
科目:初中数学 来源: 题型:
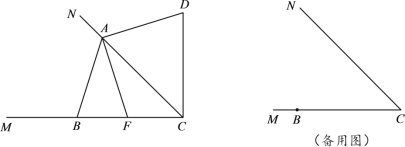
【题目】已知∠MCN=45°,点B在射线CM上,点A是射线CN上的一个动点(不与点C重合).点B关于CN的对称点为点D,连接AB、AD和CD,点F在直线BC上,且满足AF⊥AD.小明在探究图形运动的过程中发现AF=AB:始终成立.
![]() 如图,当0°<∠BAC<90°时.
如图,当0°<∠BAC<90°时.
① 求证:AF=AB;
② 用等式表示线段![]() 与
与![]() 之间的数量关系,并证明;
之间的数量关系,并证明;
![]() 当90°<∠BAC<135°时,直接用等式表示线段CF、CD与CA之间的数量关系是 .
当90°<∠BAC<135°时,直接用等式表示线段CF、CD与CA之间的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
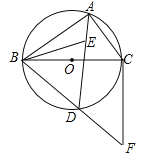
【题目】如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
(1)求证:DB=DE;
(2)求证:直线CF为⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com