
【题目】如图,点I为△ABC的内心,AB=4cm,AC=3cm,BC=2cm,将∠ACB平移,使其顶点与点I重合,则图中阴影部分的周长为( )
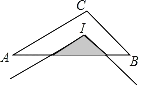
A.1cmB.2cmC.3cmD.4cm
【答案】D
【解析】
连接AI,BI,根据点I为△ABC的内心,可得IA和IB分别平分∠CAB和∠CBA,再根据∠ACB平移,使其顶点与点I重合,可得DI∥AC,EI∥BC,可得角相等,从而得等腰三角形,进而可得图中阴影部分的周长.
解:如图,连接AI,BI,
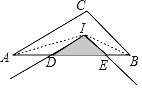
∵点I为△ABC的内心,
∴IA和IB分别平分∠CAB和∠CBA,
∴∠CAI=∠DAI,∠CBI=∠EBI,
∵将∠ACB平移,使其顶点与点I重合,
∴DI∥AC,EI∥BC,
∴∠CAI=∠DIA,∠CBI=∠EIB,
∴∠DAI=∠DIA,∠EBI=∠EIB,
∴DA=DI,EB=EI,
∴DE+DI+EI=DE+DA+EB=AB=4.
所以图中阴影部分的周长为4.
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
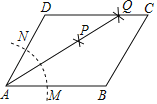
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 为
为![]() .
.
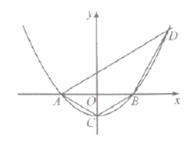
(1)求抛物线的解析式.
(2)过点![]() 作直线
作直线![]() 与抛物线在第一象限的交点为
与抛物线在第一象限的交点为![]() .当
.当![]() 时,确定直线
时,确定直线![]() 与
与![]() 的位置关系.
的位置关系.
(3)在第二象限抛物线上求一点![]() ,使
,使![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情期间,甲、乙两家网店以同样价格销售相同的防疫用品,它们的优惠方案分别为:甲店,一次性购物中超过100元后的价格部分打七折;乙店,一次性购物中超过500元后的价格部分打五折,设商品原价为![]() 元(
元(![]() ),购物应付金额为
),购物应付金额为![]() 元.
元.
(1)求出在甲店购物时![]() 与
与![]() 之间的函数解析式;
之间的函数解析式;
(2)在乙店购物时![]() 与
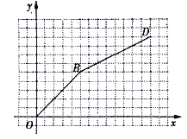
与![]() 之间的函数图像如图所示(图中线段
之间的函数图像如图所示(图中线段![]() 、射线
、射线![]() ),请在图中画出(l)中所得函数当
),请在图中画出(l)中所得函数当![]() 时的图像,并分别写出该图像与图中
时的图像,并分别写出该图像与图中![]() 、
、![]() 的交点
的交点![]() 和
和![]() 的坐标;
的坐标;
(3)根据函数图像,请直接写出新冠肺炎疫情期间选择哪家网店购物更优惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B分别在y轴和x轴上,BC⊥AB(点C和点O在直线AB的两侧),点C的坐标为(4,n)过点C的反比例函数y=![]() (x>0)的图象交边AC于点D(n+
(x>0)的图象交边AC于点D(n+![]() ,3).
,3).

(1)求反比例函数的表达式;
(2)求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定一种新的运算△:a△b=a(a+b)﹣a+b.例如,1△2=1×(1+2)﹣1+2=4.
(1)8△9= ;
(2)若x△3=11,求x的值;
(3)求代数式﹣x△4的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
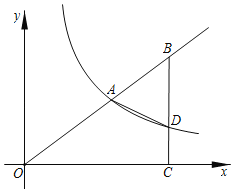
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 在反比例函数
在反比例函数![]() 的图象上,点
的图象上,点![]() 在
在![]() 的延长线上,
的延长线上,![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 与反比例函数的图象相交于点
与反比例函数的图象相交于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)求该反比例函数的解析式;
(2)若![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
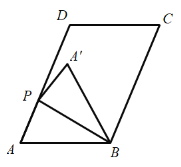
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上一点,连接
上一点,连接![]() ,沿
,沿![]() 将三角形
将三角形![]() 折叠,得三角形
折叠,得三角形![]() .
.
(1)当![]() 时,
时,![]() =_______度;
=_______度;
(2)如图,当![]() 时,求线段
时,求线段![]() 的长度;
的长度;
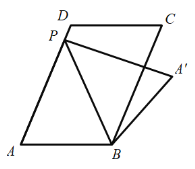
(3)当点![]() 落在平行四边形
落在平行四边形![]() 的边上时,直接写出线段
的边上时,直接写出线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
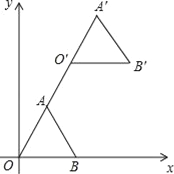
【题目】如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
A. (4,2![]() ) B. (3,3
) B. (3,3![]() ) C. (4,3
) C. (4,3![]() ) D. (3,2
) D. (3,2![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com