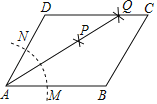
【题目】如图，在平行四边形ABCD中，按以下步骤作图：①以A为圆心，任意长为半径作弧，分别交AB，AD于点M，N；②分别以M，N为圆心，以大于
MN的长为半径作弧，两弧相交于点P；③作AP射线，交边CD于点Q，若DQ=2QC，BC=3，则平行四边形ABCD周长为________．
浙江名校名师金卷系列答案科目：初中数学 来源： 题型：
【题目】如图，⊙O的直径为AB，点C在圆周上（异于A，B），AD⊥CD．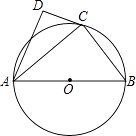
（1）若BC=3，AB=5，求AC的值；
（2）若AC是∠DAB的平分线，求证：直线CD是⊙O的切线．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场出售一批进价为2元的贺卡，在市场营销中发现此商品的日销售单价x（元）与日销售量y（个）之间有如下关系：
日销售单价x（元） | 3 | 4 | 5 | 6 |
日销售量y（个） | 20 | 15 | 12 | 10 |
（1）猜测并确定y与x之间的函数关系式，并画出图象；
（2）设经营此贺卡的销售利润为W元，求出W与x之间的函数关系式，
（3）若物价局规定此贺卡的售价最高不能超过10元/个，请你求出当日销售单价x定为多少时，才能获得最大日销售利润？最大利润是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
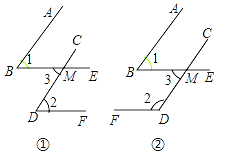
【题目】已知一个角的两边与另一个角的两边分别平行，请结合图，探索这两个角之间的关系，并说明理由．
（1）如图①，AB∥CD，BE∥DF，∠1与∠2的关系是 ；
证明：
（2）如图②，AB∥CD，BE∥DF，∠1与∠2的关系是 ；
证明：
（3）经过上述证明，我们可得出结论，如果一个角的两边与另一个角的两边分别平行，那么这两个角 ；
（4）若这两个角的两边分别平行，且一个角比另一个角的3倍少60°，则这两个角分别是多少度？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】是某汽车行驶的路程S(km)与时间t(min)的函数关系图．观察图中所提供的信息，解答下列问题：
（1）汽车在前9分钟内的平均速度是多少？
（2）汽车在中途停了多长时间？
（3）当16≤t≤30时，求S与t的函数关系式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图（1），已知：在
中，
，
，直线
经过点
，
直线，
直线，垂足分别为点
、
．证明：
．
（2）如图（2），将（1）中的条件改为：在中，，、、三点都在直线上，且
，其中
为任意锐角或钝角．请问结论是否仍然成立？如成立；请你给出证明；若不成立，请说明理由．
（3）拓展与应用：如图（3），、是直线上的两动点
、、三点互不重合），点
为
平分线上的一点，且
和
均为等边三角形，连接
、
，若
，求证：
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图（1），在平面直角坐标系中，A（a，0），C（b，2），过C作CB⊥x轴，且满足（a+b）2+
=0．
（1）求三角形ABC的面积．
（2）若过B作BD∥AC交y轴于D，且AE，DE分别平分∠CAB，∠ODB，如图2，求∠AED的度数．
（3）在y轴上是否存在点P，使得三角形ABC和三角形ACP的面积相等？若存在，求出P点坐标；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
