
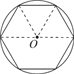
【题目】我国魏晋时期的数学家刘徽创立了“割圆术”,认为圆内接正多边形边数无限增加时,周长就越接近圆周长,由此求得了圆周率π的近似值,设半径为r的圆内接正n边形的周长为L,圆的直径为d,如图所示,当n=6时,π≈![]() =
=![]() =3,那么当n=12时,π≈
=3,那么当n=12时,π≈![]() ≈________(结果精确到0.01,参考数据:sin15°=cos75°≈0.259).
≈________(结果精确到0.01,参考数据:sin15°=cos75°≈0.259).
科目:初中数学 来源: 题型:
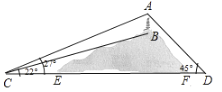
【题目】如图,山顶有一塔![]() ,塔高
,塔高![]() .计划在塔的正下方沿直线
.计划在塔的正下方沿直线![]() 开通穿山隧道
开通穿山隧道![]() .从与
.从与![]() 点相距
点相距![]() 的
的![]() 处测得
处测得![]() 、
、![]() 的仰角分别为
的仰角分别为![]() 、
、![]() ,从与
,从与![]() 点相距
点相距![]() 的
的![]() 处测得
处测得![]() 的仰角为
的仰角为![]() .求隧道
.求隧道![]() 的长度.(参考数据:
的长度.(参考数据:![]() ,
,![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情期间,甲、乙两家网店以同样价格销售相同的防疫用品,它们的优惠方案分别为:甲店,一次性购物中超过100元后的价格部分打七折;乙店,一次性购物中超过500元后的价格部分打五折,设商品原价为![]() 元(
元(![]() ),购物应付金额为
),购物应付金额为![]() 元.
元.
(1)求出在甲店购物时![]() 与
与![]() 之间的函数解析式;
之间的函数解析式;
(2)在乙店购物时![]() 与
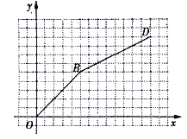
与![]() 之间的函数图像如图所示(图中线段
之间的函数图像如图所示(图中线段![]() 、射线
、射线![]() ),请在图中画出(l)中所得函数当
),请在图中画出(l)中所得函数当![]() 时的图像,并分别写出该图像与图中
时的图像,并分别写出该图像与图中![]() 、
、![]() 的交点
的交点![]() 和
和![]() 的坐标;
的坐标;
(3)根据函数图像,请直接写出新冠肺炎疫情期间选择哪家网店购物更优惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定一种新的运算△:a△b=a(a+b)﹣a+b.例如,1△2=1×(1+2)﹣1+2=4.
(1)8△9= ;
(2)若x△3=11,求x的值;
(3)求代数式﹣x△4的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
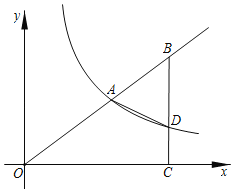
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 在反比例函数
在反比例函数![]() 的图象上,点
的图象上,点![]() 在
在![]() 的延长线上,
的延长线上,![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 与反比例函数的图象相交于点
与反比例函数的图象相交于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)求该反比例函数的解析式;
(2)若![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景
在综合实践课上,同学们以图形的平移与旋转为主题开展数学活动,如图(1),先将一张等边三角形纸片对折后剪开,得到两个互相重合的△ABD和△EFD,点E与点A重合,点B与点F重合,然后将△EFD绕点D顺时针旋转,使点F落在边AB上,如图(2),连接EC.
操作发现
(1)判断四边形BFEC的形状,并说明理由;
实践探究
(2)聪聪提出疑问:若等边三角形的边长为8,能否将图(2)中的△EFD沿BC所在的直线平移a个单位长度(规定沿射线BC方向为正),得到△![]() ,连接
,连接![]() ,
,![]() ,使得得到的四边形
,使得得到的四边形![]() 为菱形,请你帮聪聪解决这个问题,若能,请求出a的值;若不能,请说明理由。
为菱形,请你帮聪聪解决这个问题,若能,请求出a的值;若不能,请说明理由。
(3)老师提出问题:请参照聪聪的思路,若等边三角形的边长为8,将图(2)中的△EFD在平面内进行一次平移,得到△![]() ,画出平移后构造出的新图形,标明字母,说明平移及构图方法,写出你发现的一个结论,不必证明.
,画出平移后构造出的新图形,标明字母,说明平移及构图方法,写出你发现的一个结论,不必证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上一点,连接
上一点,连接![]() ,沿
,沿![]() 将三角形
将三角形![]() 折叠,得三角形
折叠,得三角形![]() .
.
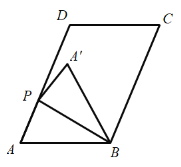
(1)当![]() 时,
时,![]() =_______度;
=_______度;
(2)如图,当![]() 时,求线段
时,求线段![]() 的长度;
的长度;
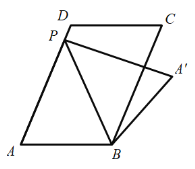
(3)当点![]() 落在平行四边形
落在平行四边形![]() 的边上时,直接写出线段
的边上时,直接写出线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2014广州)从广州到某市,可乘坐普通列车或高铁,已知高铁的行驶路程是400千米,普通列车的行驶路程是高铁的行驶路程的1.3倍.
(1)求普通列车的行驶路程;
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需要时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间甲乙两商场搞促销活动,甲商场的方案是:在一个不透明的箱子里放4个完全相同的小球,球上分别标“0元”“20元”“30元”“50元”,顾客每消费满300元就可从箱子里不放回地摸出2个球,根据两个小球所标金额之和可获相应价格的礼品;乙商场的方案是:在一个不透明的箱子里放2个完全相同的小球,球上分别标“5元”“30元”,顾客每消费满100元,就可从箱子里有放回地摸出1个球,根据小球所标金额可获相应价格的礼品.某顾客准备消费300元.
(1)请用画树状图或列表法,求出该顾客在甲商场获得礼品的总价值不低于50元的概率;
(2)判断该顾客去哪个商场消费使获得礼品的总价值不低于50元机会更大?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com